Source:
Challenging Glass 7
Conference on Architectural and Structural Applications of Glass
Belis, Bos & Louter (Eds.), Ghent University, September 2020.
Copyright © with the authors. All rights reserved.
ISBN 978-94-6366-296-3, https://doi.org/10.7480/cgc.7.4737
Authors:
Xing-er Wang
Jian Yang
Zhufeng Pan
Yuhan Zhu
Shanghai Jiao Tong University
In this work, a combined Voronoi and finite-discrete element method (FDEM) approach for reconstructing the post-fracture model of laminated glass (LG) was proposed. The fracture morphology was determined via introducing Voronoi tessellation with statistical distribution parameters such as the fragment face numbers, volume and sphericity. The residual interaction between glass fragments was described with cohesive zone model. One fractured LG block under uniaxial tension, which was taken from a triple layered LG beam with ionoplast interlayers, was modelled and validated with experimentally recorded data.
Through iteration analysis, the key cohesive parameters were determined for the most applicable model. It is followed by investigating the influence due to the fragments interaction property. The results show that the cohesion and frictional property can be combined to well describe the residual interaction behaviour between fragments. The frictional property has a remarkable effect on the post-fracture resistance whereas the associated effect on the stiffness is not evident. Compared to other cohesive parameters, the cohesive stiffness factors present predominant effect on both the post-fracture stiffness and resistance.
1. Introduction
Increasing projects of emerging glass structures, which commonly adopt multi-layered laminated glass (MLG) for load bearing components, can be found in the last decade. A typical case is to use MLG as floor plate in the glass pedestrian bridge or glass fin and beam in glass house. The structural glass is very like to be accessible or being required to survive extreme weather such as typhoon. The risks such as furniture falling and windborne debris impacts (Zhang et al. 2013; Wang et al. 2017) might cause the glass fracture. It is therefore rational to concern that if the residual post-fracture capability of structural glass components can guarantee both short term and long term performance before its replacement (Delincé 2014; Biolzi et al. 2019; D’Ambrosio et al. 2019).
Limited works can be found in both experimental and numerical study on the post-fracture performance of structural glass components. Biolzi et al. (Biolzi et al. 2016) carried out a laboratory test for examining both short term and long term behaviour of fractured SG laminated glass (LG) beam. The results show that the SG interlayer can assure the shear stress transmission between the fractured and intact glass layer. From this, the tension stiffening (TS) effect by adhesion to glass fragments can contribute to the post-fracture performance. In another experimental attempt on comparing the post-fracture performance between the MLG having Polyvinyl butyral (PVB) based interlayer (type: DG41) and combined polycarbonate-DG41 interlayer (Biolzi et al. 2018), it is found that additional polycarbonate foil can greatly increase the long term ability of the MLG beam to preserve shape.
Because the tested LG components are subjected to the in-plane load, only the positive TS effect is reported. As for the LG components under out-of-plane load, Zhao et al. (Zhao et al. 2019) tested the static post-fracture performance of both double and triple layered LG plates having various glass thermal treatment types. The results show that greater post-fracture performance can be provided if glass thermal treatment allows for generating larger fragment size. It is therefore shown that fractured float glass contribute more than tempered glass. The positive interlocking effect by holding glass fragments together via alternatively adhesion and interaction on the post-fracture capability is identified as well.
The tempered glass is hence not favourable for static post-fracture resistance when compared to float glass. Taking both the unfavourable situation of post-fracture resistance as well as the widely use of tempered glass into account, the post-fracture response of MLG using tempered glass is worth investigated. However, numerical attempts for the post-fracture model of MLG are limited compared to that for modelling the intact glass products. In Biolzi’s work (Biolzi et al. 2018), a temperature equivalence method was used to approximate the volume increase caused by the fracturing of tempered glass. From this, the negative stress field by such volume increase of fractured glass layer on the intact glass can be captured.
A more commonly used method is to simplify the fractured tempered glass as 7 equivalent undamaged glass through assuming that the tempered glass fragments are equally spaced (Galuppi, Royer-Carfagni 2018). However, such equivalent approach has limitation in modelling subsequent failure process. The fracture pattern of tempered glass presents significant stochasticity. In such pattern, the 2D glass surface is partitioned into areas dominant by convex polygons. Several attempts have been made to approximate the realistic fracture pattern of tempered glass, the typical one is to introduce Voronoi tessellation to describe the 2D fracture morphology (Pourmoghaddam, Schneider 2018; Pourmoghaddam et al. 2018; Michael Kraus et al. 2019).
This work proposes a combined Voronoi tessellation and finite-discrete element method (FDEM) approach to reconstruct the fractured tempered glass layers and further numerically model the post-fracture response of LG. The statistical distribution of various reconstruction parameters such as fragment size and sphericity can be used to adjust the fracture morphology. An iterative study of cohesive parameters for the zero-thick cohesive elements between glass fragments is firstly conducted to determine the appropriate parameters for describing the residual interaction. Finally, the influence due to the interaction behaviour between glass fragments on the post-fracture behaviour of laminated tempered glass was investigated.
2. Reconstruction concept of fractured tempered glass
2.1. Characterization of fractured tempered glass
Two aspects should be considered when characterizing the fractured tempered glass in numerical MLG model: 1) the fracture morphology of tempered glass; 2) The residual interaction behaviour between glass fragments.
The 2D fracture morphology of tempered glass, which presents dependency on the fracture initiation and the distribution of surface compressive stress, shows significant randomness. The tempered glass fragments at surface are commonly seen as convex polygons. In associated standard such as Chinese GB 15763.2 (GB 15763.2, Safety glazing materials in building - Part 2: Tempered glass 2005) and British BS EN 12150-1 (British Standards Institution 2015), a minimum number limit of glass fragments in an area of 50 mm × 50 mm, N50, is required to evaluate the quality of tempered glass product. The greater elastic strain energy U of tempered glass, which is determined by surface compressive stress and glass thickness, will lead to greater value of N50and has significant influence on the fracture intensity and fragment size distribution (Fig. 1).
Once the tempered glass fractures, most strain energy in glass will have a sudden release, which leads to the volume expansion of fractured glass layer. In the MLG, such volume expansion will be restrained due to the adhesion by the interlayer, less strain energy is then released. The unreleased strain energy as well as the irregular side facet pattern of fragments in thickness direction (Fig. 2(a)) can make the glass fragments hold together to present adequate interlocking efficiency (Fig. 2(b)). From this reason, the fractured glass layer can remain good integrity. Therefore, the residual interaction behaviour between the glass fragments cannot be neglected. In this work, the interaction behaviour between glass fragments is represented with cohesive zone model.


2.2. Voronoi tessellation for glass fragments
As the residual interaction behaviour between glass fragments is simplified and represented by zero-thick cohesive elements, the irregular side facet pattern of fragments will not be considered in this work. Only the planar fracture morphology at glass surface will be approximated and regenerated via Voronoi tessellation approach.
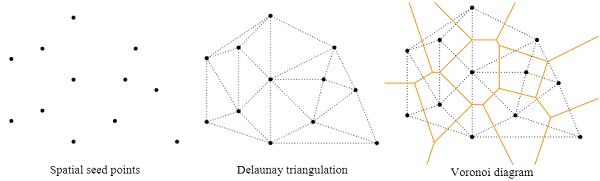
Voronoi tessellation is mathematically defined space filling geometric partitions of the computational domain, which has been extended to various research areas. A satisfactory applicability of Voronoi tessellation technique in reproducing grain based materials in different scales has been found, it is therefore widely used in associated areas such as rock mechanics. The distribution of spatial seed points, Delaunay triangulation and Voronoi decomposition are three typical steps of classic Voronoi tessellation (Fig. 3).
As the interest for various application scenarios using Voronoi tessellation grows, the Voronoi tessellation technique such as Hard-core, Centroidal and Laguerre Voronoi has been developed. For generating more realistic fracture morphology of tempered glass, a statistical distribution of characteristic seed points within each glass fragment should be determined through a large number of experimental tests on various configurations of tempered glass. The image recognition as well as image processing technique should also be adopted to capture and approximate the geometrical properties of fragments such as planar face number and area distribution.
A novel calibration framework (Michael Kraus et al. 2019), BREAK, which was recently developed by Kraus and Pourmoghaddam for predicting the planar fracture pattern of tempered glass presents promising potentials. Such framework merges both the energy criterion of linear elastic fracture mechanics and the stochastic geometry of fracture pattern. However, experimental data concerning the geometrical properties of tempered glass fragments is limited so far. Therefore, the fragment number N50 is adopted to limit the globally generated fragment number in this work. The planar fracture morphology is adjusted via manually defining various reconstruction parameters for the Voronoi tessellation.
3. Post-fracture response of laminated glass
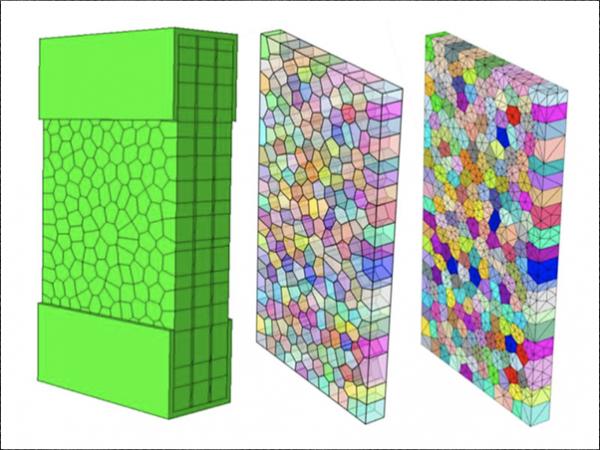
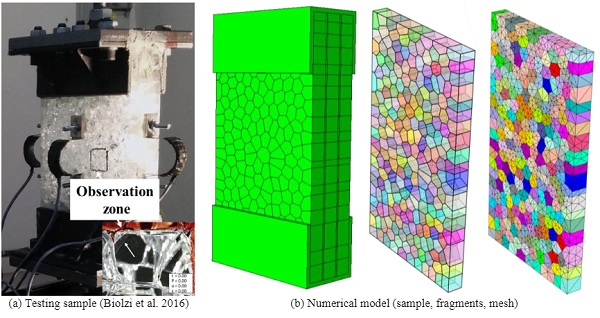
FDEM concept combined with aforementioned reconstruction approach for tempered glass fragments is introduced here to model the post-fracture behaviour of LG. The deformation of the polymeric interlayer and glass fragments will be simulated within FE framework. Once the glass fragments further separate or the debonding occurs, the contact detection and subsequent motion will be computed via explicit DEM approach. Biolzi (Biolzi et al. 2016) experimentally tested the post-fracture performance of one fracture LG block subjected to uniaxial tension, which was cut off from a triple layered LG beam with ionoplast interlayers. The numerical results from FDEM modelling will be validated with the recorded data in such test.
3.1. FDEM model of fractured laminated glass
The LG block is laminated by three tempered glass of 12 mm and two ionoplast interlayers (SG) of 1.52 mm, which is cut off from a fractured LG beam. The total size of LG block is 180mm × 100 mm × 39.04 mm (Fig. 4(a)). From the observation zone in Fig. 6 (a), the average fragment size is around 8 mm, which is similar to that in case UT3 (U = 104.1J·m-2 in Fig. 1). The statistical reconstruction parameters adopted for the fractured glass layer are listed in Table 1. The numerical model including the numerical sample, reconstructed fragments and mesh is shown in Fig. 4(b).
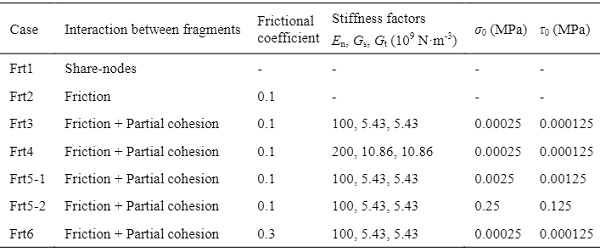
Table 1: Interaction property between glass fragments.

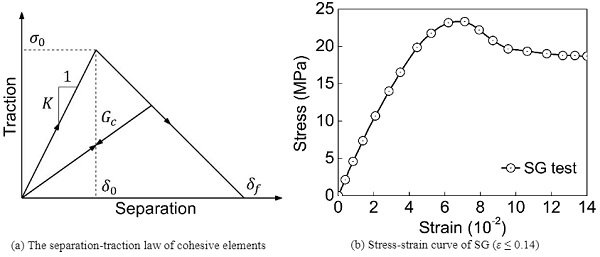
In order to adjust the interaction between fragments from cohesion dominant behaviour to friction dominant behaviour, cohesive elements of zero-thickness are inserted between neighbouring fragments. A bilinear separation-traction law (Fig. 5(a)) is employed for zero-thick 6-Node three-dimensional cohesive elements. The key cohesive parameters are fracture energy Gc, cohesive characteristic strength (normal characteristic strength σ0 and tangential characteristic strength τ0), cohesive stiffness factor K.
The cohesive parameters are subsequently iteratively analysed to determine one applicable set to map with experimental results. A mesh with 32742 solid 4-Node linear tetrahedron elements is adopted for fractured glass layers. As the LG block is under uniaxial tension, the secondary breakage of glass fragments will not be observed. The glass fragments are then seen to be intact and elastic.
The material property of ionoplast interlayer is taken from the testing data of Biolzi’s work (Biolzi et al. 2016). The stress-strain relationship, of which the strain ε is less than the peak recorded strain of 0.14 in the experiment is shown in Fig. 5(b). The potential interfacial debonding between fractured glass layers and ionoplast interlayers is found to greatly influence the post-fracture stiffness as reported in Galuppi’s analytical efforts (Galuppi, Royer-Carfagni 2016). The cohesive zone model with bilinear separation-traction law is invoked to capture the interfacial bonding behaviour as well.
Because of the limitation in experimentally identifying both Mode I and Mode II bonding behaviour between ionoplast interlayer and glass, similar interfacial property are adopted as PVB based interface reported in Ref (Pelfrene et al. 2015; Samieian et al. 2019), the interfacial characteristic strength σ1 and τ1 are 10 MPa and 5 MPa in the reference case, respectively. It is noted that, as the reported fracture energy for PVB delamination from tests has a great variation according to the loading rate. In Samieian’s work (Samieian et al. 2019), Gc1 ranges from around 400 N·m-1 at test rate less than 1 s-1to more than 3000 N·m-1at test rate greater than 10 s-1 when the temperature is around 20 °C.
Pelfrene collected the testing data from other publications and suggested that an available value Gc1 of around 800 N·m-1 can be used for medium bond level of PVB bonding interface (Pelfrene et al. 2015). In addition, it seems that Gc1 for SG bonding interface can hardly be found which might be due to its strong adhesion that will lead to the fracture of glass substrate before delamination. It is believed that Gc1for SG bonding interface is greater than that for PVB interface. Thus, considering the reported data so far, the fracture energy Gc1 for delamination in all modes is set as 1000 N·m-1in this work.
3.2. Effect of interaction behaviour between fragments
Six interaction conditions are considered in the numerical models for exploring the effects of interaction between fragments and associated cohesive parameters on the post-fracture behaviour. The interaction conditions examined are as follows:
1) Frt1: Glass is intact without breakage;
2) Frt2: Only friction behaviour, which is computed via penalty friction approach is considered. The penalty frictional coefficient is 0.1;
3) Frt3: In addition to the penalty friction, partial cohesion is considered. Frt3 is the reference case after iterative analysis, i.e. Frt3 achieves the satisfactory agreement with the experimental results;
4) Frt4: The cohesive stiffness factors are twice that in Frt3. The cohesive characteristic strength is identical to that in Frt3;
5) Frt5: The cohesive stiffness factors are identical to that in Frt3 via scaling the cohesive characteristic strength and fracture energy. Two cases, Frt5-1 and Frt5-2 are defined to examine the influence due to different scaling factors;
6) Frt6: The friction coefficient is 0.3. The cohesive property is identical to that in Frt3.
The interaction property between glass fragments is given in Table 2.
Table 2: Interaction property between glass fragments.
In Biolzi’s test, the fracture LG block is tested under repeated loads with various load speed. Four typical testing records under fast (Tests 3 and 4) or slow load speed (Tests 1 and 2) are given in Fig. 6.In Ref (Biolzi et al. 2016), only the tensile deformation of LG block less than nominal strain of 0.04 is tested and provided. Testing stresses are calculated without considering the cross section of fractured glass.
It is also shown that the strain-stress curve of fractured LG block will finally follow the same path as that of SG test when fragments are fully separated and delaminated. Therefore, the recorded curves of Tests 2 and 4 are linearly extended to intersect with that of SG test. The shaded area between the curves of Tests 2 and 4 is seen as the most potential area that can cover the stress-strain relationship from both experimental and numerical results.
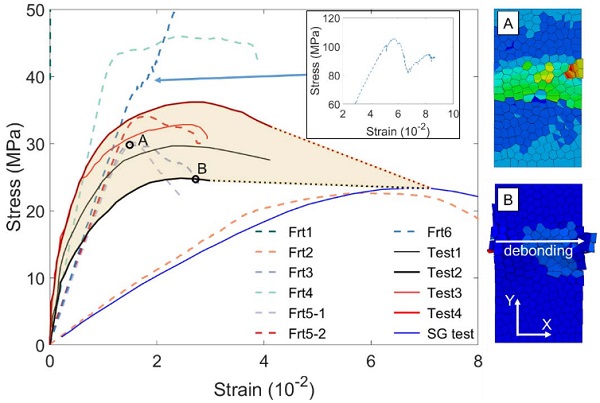
The nuemrical results from fragments interaction cases are shown in Fig. 6. Through trials and errors tests on determining the interaction property as well as the sensitivity study on the load speed, the Frt3 case is taken as the reference case. From the stress-strain curve of Frt3, it can be seen that Frt3 has a peak stress of 29.8 MPa at Point A which is identical to that in Test 1. Before reaching the peak stress, Frt3 has a linear stiffness of nearly 2.19 GPa. In the following discussion, such linear stiffness will be taken as the equivalent stiffness in the post-fracture stage. It is noted that, differing from the numerical results, the experimental data shows that the stress-strain relationship always presents nonlinearity and is more plastic-like.
This might be due to the gradual movement and separation of adjacent fragment-clusters, which leads to such plastic-like behavior when SG polymer is still linear elastic before yielding. Because numerical model shows the difficitulties in modeling such movement and Frt3 case achieves the most consistent results under various load speed, the Frt3 case is therefore seen acceptable and acts as reference case. The stress-strain curve of Frt3 case intersects with the lower bound of shaded area at Point B, where the debonding area finally propagates through the LG block along X direction. The interlocking effect of fragments will greatly decrease after Point B. The subsequent resistance will mostly depend on the SG interlayer and TS effect.
The equivalent stiffness of Frt1 case is much greater than other cases as it represents the intact case. The mean stiffness will be 64.5 GPa if the cross section of glass layers are introduced in calculating stress, which is close to that of 66.96 GPa in Ref (Biolzi et al. 2016). In Frt2 case, the fragments interaction is simplified to frictional behavior. It can be seen that the equivalent stiffness is around 534 MPa, which has a slight increase of 16% than that of 460 MPa in SG test. This shows single frictional behavior cannot well describe the fragments interaction. Because of the strong contact force between fragments due to the volumn expansion, a prestress field might be required to apply initial normal force for the frictional behavior if partial cohesion is not invoked.
The equivalent stiffness in Frt4 caseis 3.9 GPa, which has a 78% increase when comparing with that in Frt3 case. The peak stress also rises to nearly 46 MPa of 54% increase. The results show that the cohesive stiffness factors have significant effect on both the equivalent stiffness and peak stress. It can also be observed that the stress-strain curve after the linear stage is rather stable, which has a good agreement with the experimental data. However, it is rational to predict that such stable stage will be transformed to a more rapid decline that is similar to Frt3 case, if decreasing the cohesive stiffness factors for reducing the peak stress.
In Frt5 cases, different scaling factors of cohesive characteristic strength and fracture energy are set to examine the associated influence on the stress-strain relationship. From Fig. 6, compared to that in Frt3, the stress declines faster in Frt5-1 case after the peak where as the peak stress and equivalent stiffness is almost identical to that in Frt3. In Frt5-2, the peak stress increases to 34 MPa as the rise of equivalent stiffness is negligible. It can then be found that, once the cohesive stiffness is determined, the scaling factors do not have significant influence on the post-fracture equivalent stiffness. However, the adjustment of scaling factors can still contribute to the peak stress and subsequent behaviour.
The increase of friction coefficient from 0.1 to 0.3 leads to a remarkable rise of peak stress, which increases from 29.8 MPa in Frt3 to 105 MPa in Frt6 (see inset figure in Fig. 6). The equivalent stiffness (2.45 GPa) does not show great sensitivity on the variation of friction coefficient. Comparing Frt2, Frt6 with the reference case Frt3, it can be found that the friction behaviour will greatly affect the peak stress of fractured LG block where as the corresponding effects on the post-fracture equivalent stiffness are not evident.
4. Concluding remarks
In this work, a combined Voronoi-FDEM approach was proposed for generating the post-fracture model of laminated tempered glass. Such reconstruction approach was then used to reproduce fractured tempered glass and further model the mechanical behaviour of fractured laminated tempered glass. The key cohesive parameters of the numerical model were determined by calibrating with the experimental data. The influence due to fragments interaction property on the post-fracture behaviour of laminated tempered glass was examined. The results show that:
The fragments interaction due to the volume expansion and irregular side facet pattern of fragments cannot be well described by single frictional behavior. Other types of interaction property such as cohesion should be introduced to model the residual interaction. However, the sensitivity study shows that the friction coefficient will greatly affect the post-fracture resistance where as the corresponding effect on the post-fracture stiffness is not evident.
The cohesvie stiffness factors present significant effect on both the post-fracture stiffness and resistance. Once the cohesive stiffness factors are determined, the scaling factors for adjusting fracture energy and charateristic strength of fragments interaction property will not have remarkable influence on the post-fracture stiffness.
5. Acknowledgement
This work was supported by the National Key Research and Development Program of China [Grant No. 2017YFC0806100], the National Natural Science Foundation of China [Grant No. 51908352] and the project of Key Laboratory of Impact and Safety Engineering (Ningbo University), Ministry of Education [Grant No. CJ201906].
6. References
Biolzi, L., Casolo, S., Orlando, M., Tateo, V.: Modelling theresponse of a laminated tempered glass for different configurations of damageby a rigid body spring model. Eng.Fract.Mech.218, 106596 (2019). doi:https://doi.org/10.1016/j.engfracmech.2019.106596
Biolzi, L., Cattaneo, S., Orlando, M., Piscitelli, L.R., Spinelli, P.: Post-failure behavior of laminated glass beams using different interlayers. Compos.Struct.202, 578-589 (2018). doi:https://doi.org/10.1016/j.compstruct.2018.03.009
Biolzi, L., Orlando, M., Piscitelli, L.R., Spinelli, P.: Static and dynamic response of progressively damaged ionoplast laminated glass beams. Compos.Struct.157, 337-347 (2016). doi:https://doi.org/10.1016/j.compstruct.2016.09.004
British Standards Institution: BS EN 12150-1, Glass in building -Thermally toughened soda lime silicate safety glass Part 1: Definition anddescription. In.BSI Standards Limited, London, (2015)
D’Ambrosio, G., Galuppi, L., Royer-Carfagni, G.: A simple model for the post-breakage response of laminated glass under in-plane loading. Compos.Struct.230, 111426 (2019). doi:https://doi.org/10.1016/j.compstruct.2019.111426
Delincé, D.: Experimental approaches for assessing time and temperature dependent performances of fractured laminated safety glass. Ghent University (2014)
Galuppi, L., Royer-Carfagni, G.: A homogenized model for the post-breakage tensile behavior of laminated glass. Compos.Struct.154, 600-615 (2016). doi:https://doi.org/10.1016/j.compstruct.2016.07.052
Galuppi, L., Royer-Carfagni, G.: The post-breakage response of laminated heat-treated glass under in plane and out of plane loading. Compos.Part B: Eng.147,227-239 (2018). doi:https://doi.org/10.1016/j.compositesb.2018.04.005
GB 15763.2, Safety glazing materials in building -Part 2: Tempered glass. In. Standards Press of China, Beijing, (2005)
Michael Kraus, Navid Pourmoghaddam, Jens Schneider, Geralt Siebert: BREAK–Calibrating Stochastic Tessellations for the Prediction of Fracture Patterns of Thermally Pre-stressed Glass. Paper presented at the Glass Performance Days, Tampere(2019)
Nielsen, J.H., Bjarrum, M.: Deformations and strain energy in fragments of tempered glass: experimental and numerical investigation. Glass Struct.Eng.2(2), 133-146 (2017). doi:10.1007/s40940-017-0043-8
O'Regan, C.: Structural use of glass in buildings (Second edition). IStructE Ltd, London (2014)
Pelfrene, J., Van Dam, S., Van Paepegem, W.: Numerical analysis of the peel test for characterisation of interfacial debonding in laminated glass. Int.J.Adhes.Adhes.62, 146-153 (2015). doi:https://doi.org/10.1016/j.ijadhadh.2015.07.010
Pourmoghaddam, N., Kraus, M.A., Schneider, J., Siebert, G.: Relationship between strain energy and fracture pattern morphology of thermally tempered glass for the prediction of the 2D macro-scale fragmentation of glass. Glass Struct.Eng.1-19 (2018). doi:10.1007/s40940-018-00091-1
Pourmoghaddam, N., Schneider, J.: Experimental investigation into the fragment size of tempered glass. Glass Struct. Eng.3(2), 167-181 (2018). doi:10.1007/s40940-018-0062-0
Samieian, M.A., Cormie, D., Smith, D., Wholey, W., Blackman, B.R.K., Dear, J.P., Hooper, P.A.: On the bonding between glass and PVB in laminated glass. Eng.Fract.Mech.214, 504-519 (2019). doi:https://doi.org/10.1016/j.engfracmech.2019.04.006
Wang, X.-e., Yang, J., Liu, Q.-f., Zhang, Y.-m., Zhao, C.: A comparative study of numerical modelling techniques for the fracture of brittle materials with specific reference to glass. Eng.Struct.152, 493-505 (2017). doi:https://doi.org/10.1016/j.engstruct.2017.08.050
Zhang, X., Hao, H., Ma, G.: Laboratory test and numerical simulation of laminated glass window vulnerability to debris impact. Int.J.Impact Eng.55(5), 49-62 (2013)
Zhao, C., Yang, J., Wang, X.-e., Azim, I.: Experimental investigation into the post-breakage performance of pre-cracked laminated glass plates. Constr.Build.Mater.224, 996-1006 (2019). doi:https://doi.org/10.1016/j.conbuildmat.2019.07.286