This paper was first presented at GPD 2017 by Laura Galuppi and Gianni Royer Carfagni.
A homogenized approach is presented that fits the case of broken tempered glass, characterized by small shards approximately of the same size. The tension stiffening is evaluated as a stress perturbation, determined within a class of shape functions though complementary energy minimization. This provides accurate estimates for the postbreakage in-plane effective-stiffness, which strongly depends, besides the interlayer stiffness, upon fragment size and glass-topolymer adhesion. An extension of the model to the case of broken laminated glass plates under equi-biaxial loading.
The strength of the proposed method consists in the possibility of accounting for the stress diffusion phenomena in simple mathematical terms, allowing to reach simple formulas for the estimation of the effective stiffness of laminated glass in the post-breakage phase. Comparisons with numerical experiments confirm the accuracy of the proposed homogenized approach.
Introduction
When used for structural purposes, glass is often of a safety type, a category that includes laminated glass, a composite formed by two (or more) glass plies bonded by thin polymeric interlayers with a process at high temperature and pressure in autoclave. The role of the interlayer is twofold.
In the pre-glass breakage phase it allows the transfer of shear stresses between the glass plies, ensuring that the flexural inertia of the laminated glass element is higher than the sum of the inertiae of the isolated glass plies. In the post-glass breakage phase, the glass shards remain attached to the polymer so that the assembly maintains a certain cohesion. This provides a small but significant load bearing capacity, avoiding injuries due to catastrophic collapse.
A large number of theoretical and experimental studies have been devoted to the evaluation of the properties of sound laminated glass, while very few are the contributions for the post-breakage response, although this is strongly associated with the safety requirements, mainly ruled by impact and dynamic performance.
Indeed, many standards prescribe to use for structural glass the fail safe design approach, typical in aircraft design, where it is accepted that one or more components may fail in extreme situations, but without compromising the overall stability of the structural system. Its goal is to verify that, in case of partial or total fragmentation of glass components as a result of accidental actions, a sufficient stiffness and strength is maintained to withstand self-weight and dead loads, as well as a fraction of the live loads, thereby preventing danger from falling materials.
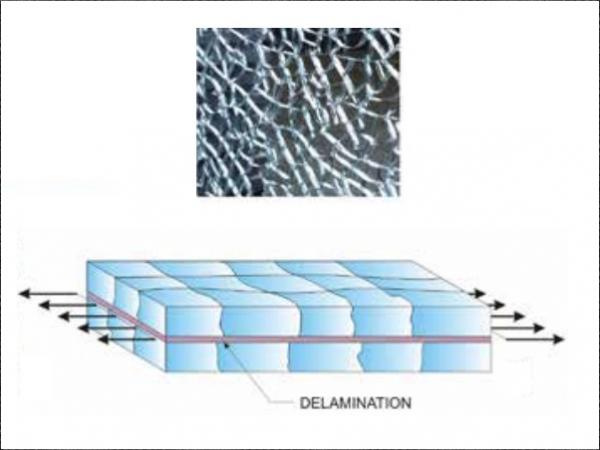
The laminated glass response in the postcritical phase is highly dependent on the bridging between adjacent glass fragments ensured by the polymer, and results from a combination of the elongation of the interlayer and the delamination from the glass shards near the cracks. Henceforth, factors that influence the post-breakage response are
• glass-interlayer adhesion properties;
• interlayer stiffness, depending upon polymer type, temperature and load duration;
• size and shape of the glass fragments, which are influenced by the type of glass, treatments to which it has been subjected, glass thickness, type of load, loading rate and type of constraints.
Remarkably, the adherence with the glass fragments produces the tension stiffening of the polymeric film, which otherwise would present negligible mechanical performance.
In [1] an innovative method, based on a proper development of the perturbation approach first proposed by Hashin [2], is presented to evaluate the post-breakage effective stiffness of laminated glass panels under uniaxial in-plane loading, i.e., to find the elastic modulus of an equivalent homogeneous body with the same tensile properties of the broken laminated element. The considered scenario is specifically representative of thermally toughened and heat strengthened glass, characterized by the presence of small fragments, invading the entire panel, and accounts for the glass-interlayer delamination.
The proposed model starts from the analytical evaluation of the stress state in the interlayer, that turns out to be strongly influenced by the contact with the glass shards. In [3], the study has been extended to the case of broken laminated glass under equi-biaxial state of stress.
Broken laminated glass under tensile stress. The model problem
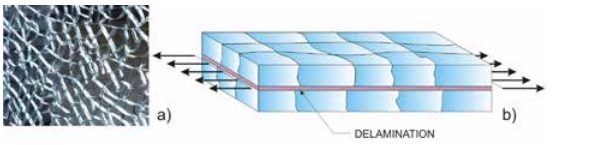
In the post-glass-breakage phase, thermallytoughened and heat-strengthened laminated glass can be regarded as a composite formed by the interlayer to which randomly distributed glass shards remain adherent (Fig. 1a), with homogeneously distributed fragmentation.
As shown in Fig. 1b, we will consider first the case in which the element is uniaxially loaded approximately in the same direction of the dominant cracks. Clearly, the cracks whose plane is parallel to the direction of loading are subject to null or negative opening stress (due to the lateral contraction of the interlayer), so that they do not influence the tensile response. Therefore, one can consider only the effects of the cracks orthogonal to the tensile stress and the problem may be studied as a two-dimensional case, in plane stress or plane strain.
The considered reference geometry is a broken laminated glass element composed by two glass plies of the same thickness, bonded by a polymeric interlayer of thickness 2t and Young’s modulus Ep. Let us consider as reference element, the region comprised between two consecutive cracks, of length 2a, shown in Fig. 2. Any two consecutive glass fragments are bridged by the ligament of the polymeric interlayer and the tensile response is governed by the interlayer stiffness and adhesion.
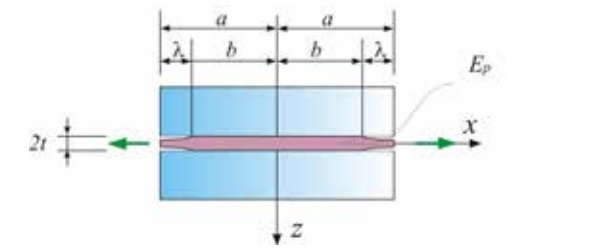
The same figure also evidences that each glass fragment is assumed to be symmetrically detached at its ends for a length λ and, hence, bonded to the interlayer in the central zone of length 2b = 2 (a-λ).
To our knowledge, the only formula available in the literature [4] defines the equivalent Young's modulus Eeq of cracked laminated glass, stiffened by the adhesion with the glass shards, as a function of the interlayer modulus Ep, of the fragment size L and of the glass/polymer debond length λ, in the form

The undelaying hypothesis in this approach is that the strain in the interlayer is null in the bonded zones, and uniaxial in the remaining parts. In our approach, we will instead consider the stress diffusion between the bonded and unbonded parts.
Evaluation of the stress state in the interlayer
Since the elastic modulus of glass (70 GPa) is much higher than that of the interlayer (strongly dependent on temperature and load duration, but of the order of 10 MPa), the glass shards can be considered rigid with respect to the polymer and the analysis may focus on the interlayer only.
In particular, the isolated interlayer may be regarded as the reference configuration, in which it is subjected to a homogeneous state of stress δ while the actual state of stress δ is the sum of the reference stress and a perturbation stress arising from the contact with the glass fragments, i.e.,
![]()
The perturbation stress is evaluated in [1], under the simplifying assumption of constantthrough-the thickness axial stress, by means of energy minimization methods. Fig. 3a shows a qualitative plot of the obtained solution, according to which the mean axial stress in the interlayer turns out to be constant in the external detached zones, where the presence of the glass fragments does not lead to stress perturbations. The stress distribution is characterized by a stress diffusion phenomena inside the bonded region, which depends upon the bond length, the interlayer thickness and its Poisson’s ratio.
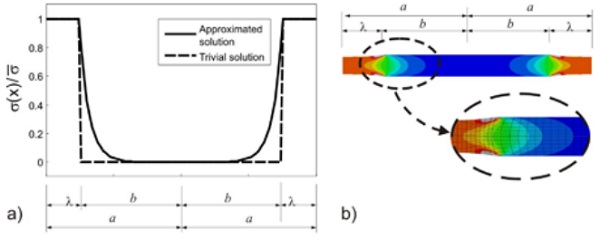
In the same figure, a trivial solution is plotted for the sake of comparison. This solution, leading to the simplified formula (1) for the effective stiffness of the beam, considers that only the detached zones of the interlayer contribute to the elongation of the element, while the contact with the glass fragments prevents the elongation of the interlayer in the bonded zones. Obviously, this approach completely neglects the stress diffusion phenomena, that, on the other hand, are confirmed by numerical experiments, as shown by Fig.3b.
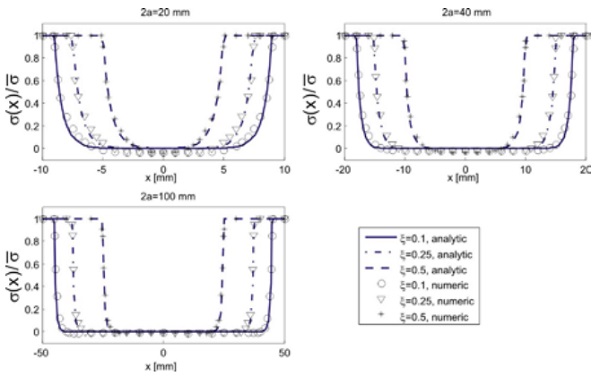
Comparisons of the obtained average stress with that evaluated numerically, by means of accurate analyses performed with the code Abaqus, are shown Fig. 4 and discussed in detail in [1], for different values of the fragment size and of the delamination length.
In general, the stress diffusion phenomenon is the more important the lower the length of the glass shards is.
Effective stiffness of the broken laminated glass element under tensile load
To facilitate the structural calculations, it is convenient to introduce average properties of the damage elements. Here, we define the effective stiffness of the cracked laminate under tension as the stiffness of a homogeneous body with the same geometry of the interlayer, presenting the same tensile properties in terms of elongation. It is determined by introducing the effective Young’s modulus Eeq.
As discussed in [1], a lower bound for the effective stiffness may be found, starting for the perturbed stress state (2), by means of energy theorems, in the form

where χ(a,λ,t) is a non-dimensional quantity, depending on the detachment length, the glass fragment size and the interlayer thickness. It may be regarded as a corrective coefficient for formula (1). Accurate charts for the determination of such a coefficient are proposed in [5].
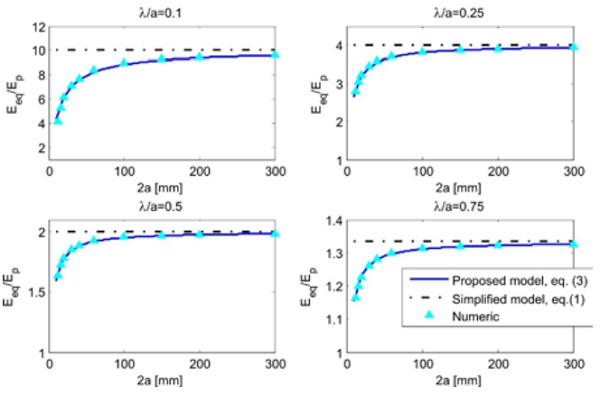
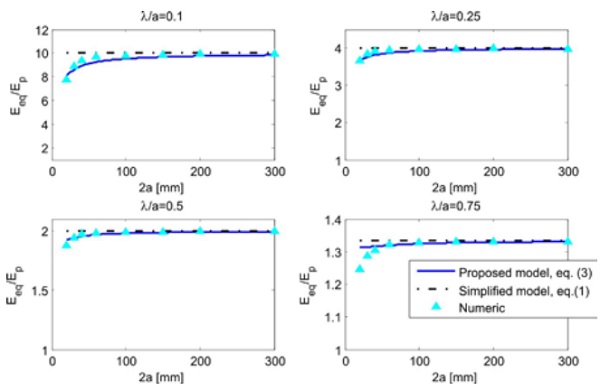
The graphs of Fig. 5 and Fig. 6 show Eeq, normalized by the interlayer elastic modulus Ep, as a function of the fragment length 2a for different values of λ/a (representing the percentage of detached interlayer) for interlayer thickness of 1,52 mm, and for plane stress and plane strain conditions, respectively. Numerical results, obtained by means of numerical analyses performed with the program Abaqus, and values from the simplified model of [1] are compared in the same graphs. By comparing those Figures, it may be observed that, for plane strain conditions, the dependence of the effective modulus on the fragment length is less pronounced than in the plane stress conditions.
Observe that the simple model of eq. (1) provides values of Eeq independent of the glass fragment length, which are correlated only with the parameter λ/a. In general the corresponding estimate is not accurate.
On the other hand, it is evident that the estimate from (3) is very close to the numeric results. The mean error, considering the range 2a = [20mm÷300mm] and λ/a = [0.1÷0.9], is less than 4% for plane stress, and of the order of 1% for plane strain conditions.
It may be observed that the analytic prediction for the lower bound of Eeq results to be higher than the numerical calculation for high values of λ/a and low values of a. Here, the model indicates a stiffening of the element, which is not predicted by the numerical analysis.
This discrepancy is associated with the phenomenon of stress diffusion in the bonded zone of the interlayer: when the bond length is very small the two stress-diffusion zones tend to merge, so that part of the axial load directly flows through the interlayer, with no need of being transferred to the adherent glass fragments. The proposed analytical model, based upon the constant-in-the-thickness axial stress approximation, cannot correctly capture this effect. However, this is a limit condition, certainly of minor practical interest.
Response under equi-biaxial loading
Let us consider now a cracked laminated glass panel subjected to equi-biaxal loading, as shown by Fig. 7a, assuming that the fragmentation is homogeneously distributed, so that all the cracks are subjected to the same positive opening stress. The representative element, shown in Fig. 7b, comprised between cracks, is assumed to be the square, 2a x 2a, while the shape of the central bonded region has been evaluated by means on numerical experiments [3] and turns out to be circular, with radius R.
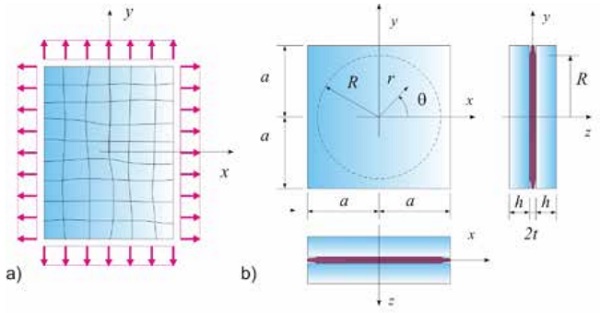
Following a procedure similar to that described for the case of beam under tensile load, the perturbed stress state in the interlayer is evaluated through a perturbation approach, while a lower bound for the effective stiffness of the broken laminate may be obtained by means of energetic methods, and reads
![]()
where, again, χ(a,R,t) is a non-dimensional coefficient, depending on the fragment size, the radius of the bonded region and the interlayer thickness.
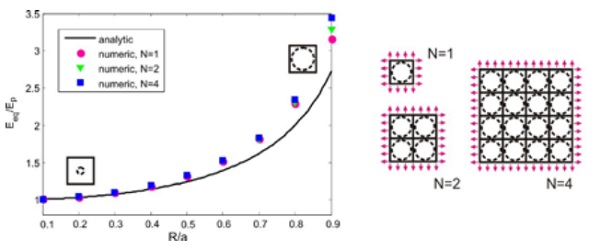
With respect to the case of beam under tensile load, for the 2D problem of plate under equi-biaxial load, the interaction among adjacent cells represents an important issue. This is shown in Fig. 7 , where the numerical results, in terms of effective elastic modulus Eeq (normalized by the interlayer modulus Ep) are plotted as a function of R/a, for fragment are plotted as a function of elementary cells N. Results obtained through equation (4) are plotted in the same graphs.
The numerical analyses show that, by increasing N, the effective stiffness increases, being the phenomenon more pronounced for high values of R/a. This is due to the fact that, when the number of elements is high, the stress state of the detached zones turns out to be perturbed by the presence of the adjacent fragments and, hence, the stiffening actions of the glass fragments interact one other.
This effect is more marked for high values of R/a because the different bonded regions are closer one another. Phenomena of this kind cannot be caught by the analytical approach. However, it may be verified that of the error in the evaluation of Eeq with the analytical approach strongly depends upon R/a, while its dependence on N is less evident. In practice, if the approximation for the effective stiffness is considered to be acceptable independently of the panel size. Analogous analyses performed by considering different values of the glass fragment size confirm that the cracked element response is almost independent of the glass fragment size, as found analytically.
Conclusions
An innovative method has been presented to evaluate the post-breakage effective stiffness of laminated glass panels under uniaxial tensile loading, either in generalized plane stress or plane strain conditions. The polymeric interayer foil is stiffened by the contact with the adherent glass shards, but partial delamination is supposed to occur at the interface. The model can take into account the complicated stress distribution from the detached zones, in which the shards are bridged by the interlayer-ligament only, to the regions where glass is bonded to the interlayer.
Such a phenomenon, which does not seem to have been properly considered in previous studies, provides a stiffening effect for the cracked laminated glass that depends upon the interlayer thickness, the characteristic size of the glass shards and the length of the bonded zone. The method has been extended to the study of the response of broken laminated glass plates under equi-biaxial state of stress.
In both cases, the proposed model allows a simple evaluation of the effective stiffness of broken laminated glass element under tension, permitting to reach simple expressions for the elastic modulus of a homogeneous body with the same tensile properties. This study has confirmed that the response of the damaged panel is governed by the presence of the delaminated regions, and by the interface conditions with the bonded zone, as well as on the interlayer properties and thickness.
Comparisons of the obtained results with accurate numerical experiments confirm the accuracy of the proposed approach. The errors in the considered case-studies are of the order of a few percentage.
This study is certainly propaedeutic for the analysis of the bending response of laminated glass beams, as well as of damaged glass panels under out-of-plane equibiaxial flexure, like the situation occurring in the ring-on-ring testing methods for glass strength suggested by standards EN-1288-2 and EN-1288-5.
References
[1] L. Galuppi, G. Royer-Carfagni, 2016. A homogenized model for the post-breakage tensile behavior of laminated glass. Compos Struct 154, pp. 600–615. [2] Z. Hashin, 1985. Analysis of cracked laminates: a variational approach. Mech Mater 4(2), pp. 121-136.
[3] L. Galuppi, G. Royer-Carfagni, 2017. A homogenized analysis à la Hashin for cracked laminates under equi-biaxial stress. Applications to laminated glass. Compos Part B – Eng 111, pp. 332-347.
[4] S.J. Bennison, I. Stelzer, 2009. Structural properties of laminated glass. Short Course, Glass Performance Days, Tampere (Finland).
[5] L. Galuppi, G. Royer-Carfagni, 2017. Modelling the post-breakage response of laminated glass. Analogies with reinforced concrete mechanics. Submitted.