Authors: Liene Sable, David Kinsella and Marcin Kozłowski
Source: International Journal of Structural Glass and Advanced Materials Research, Volume 3 No. 1, 2019, Science Publications
DOI: https://doi.org/10.3844/sgamrsp.2019.62.78
Abstract
Architectural trends increasingly challenge material producers and engineers to create sustainable, renewable and innovative laminated glass products that combine multiple functions as in, for example, glass railings with solar cells, curved laminated glass, floors with light emitting diodes that serve as multimedia screens. All new tendencies require the development of interlayers for laminated glass, which allows laminating electrical parts, solar cells or other objects between two glass plies. For this complex lamination process, the most appropriate interlayer is Ethylene Vinyl Acetate (EVA), because its properties allow for working in low temperatures without autoclave. From the other hand, EVA material has not been defined and discussed entirely in prEN16613 standard as a suitable interlayer material, for example, for structures application like Polyvinyl Butyral (PVB) interlayer. For this reason, EVA interlayer laminates must be investigated and compared with PVB or similar interlayer laminates to evaluate its mechanical behaviour.
The research paper gives an idea and compares the structural behaviour and fracture pattern and evaluates laminated glass samples with PVB, Ionoplast and EVA interlayers. Under practical circumstances, glass structures need to be designed to withstand bending stresses which may occur, e.g., due to lateral loading, that means that four-point bending tests is appropriate method for the evaluation of structural behavior. Tests were also modelled in the Finite Element (FE) ABAQUS/CAE software to calculate displacements and evaluate bending stresses. According to current research, the conclusion can be drawn that for samples with EVA interlayer, stiffness is equivalent to PVB interlayer specimens’ results and EVA interlayer can be used in the same cases as PVB material. Moreover, using FE method makes it possible to simulate accurately the mechanical behaviour of laminated glass tested in 4-point bending with high result correlation with error less than 5% while the analytical calculations show error of 10-58%.
Introduction
Significant development of structural glass has been observed during last decades. Glass material is not just used as insulated glass infill units, but it is a fully-responsible structural material. (Eekhout and Sluis, 2014; Grohmann, 2014; Raynaud, 2014) Compared to monolithic glass sheet, laminated glass after collapse maintains its integrity and the structure can perform its function until it is replaced. The laminated glass is a composite material, which consists of at least two plies of glass bonded together with polymer interlayer. Selection of interlayer type most often depends on the application of the structural element, for example, impact resistant, acoustic insulating, burglar safe or fire resistant (Sandén, 2015).
From the structural point of view, glass is a brittle material and fails without warning. It is sensitive to stress concentrations and its strength depends on the degree of damage to the glass surface (Pfaender, 1996). The tensile strength is governed by the presence of material flaws, which magnify the stresses locally and act as potential failure sites. The stressraising property of a flaw is dependent on its shape and size, which, however, cannot be properly, determined using measurement technology available at present (Lamon, 2016).
Interlayer integration between glass plies is one of possibilities to maintain the load-bearing capacity and structural integrity after glass breakage. The advantage of polymer interlayer is its ability to absorb large deformations, retain glass splinters and limit the size of gap between glass shards after glass failure.
In this paper, the structural behaviour and fracture patterns are investigated for samples with different types of interlayers: Polyvinyl Butyral (PVB), Ethylene Vinyl Acetate (EVA) and Ionoplast. These are alternative polymers for laminated glass applications. The oldest and most used interlayer material in structures and automotive industry is PVB, while EVA is mostly used for photovoltaic modules like encapsulant material (El Amrani et al., 2007). It is because of its relatively low production temperature and the possibility to laminate decorative or electric (for example, light diode) features. Every type of interlayer has specific application (Sandén, 2015) purpose and these factors determine what kind of mechanical properties and material characteristics are required.
For laminated glass analytical bending stresses and deflection determination, an “effective thickness” method has been developed. Mainly three versions in practice are used-standards ASTM 1300, prEN 16612 and Enhanced Effective Thickness approach (EET) by Galuppi and Royer-Carfagni (2012).
The basic principle for the ASTME1300 approach is to determine two different laminate effective thickness values, one is used for the calculation of deflection and the other for glass stress. This method includes formulas for the precise determination of the interlayer shear transfer coefficient, Γ. The effective laminate thickness approach provides the equivalent monolithic thickness for stiff interlayers (Γ→1) and the layered limit for compliant interlayers (Γ→0). (ASTM 1300, 2010) The method applies mostly for 2- ply laminates made from equal and unequal thickness of glass plies.
The concept of “stiffness families” are presented in the draft of European norm for glass (prEN 16612, 2017; prEN16613, 2017). The main idea of this approach is the classification into “stiffness families“, moreover, the interlayer family determines the coefficient of shear transfer ω. Basically, this is the same approach as included in ASTM 1300-16 as the value of Γ. In this case, the interlayer producer defines Young’s modulus and Poisson’s ratio, which is a function of the temperature and the characteristic duration of the load. Regulations provide three main “stiffness families” for interlayers-“non-described” and “acoustic” (Family 0), “standard grade PVB” (Family 1) and “structural” (Family 2) interlayers. (prEN 16612, 2017) However, this standard does not define the family for EVA interlayer but it can be evaluated according to (prEN16613, 2017) and interlayer material properties.
The third method is Enhanced Effective Thickness approach (EET) suitable for the evaluation of the effective thickness for both “beam” and “plate” geometries. By choosing appropriate shape functions for the laminated-beam deformation, minimization of the strain energy functional gives new expressions for the effective thickness under any constraint- and loadconditions, embracing the classical formulations as particular cases (Galuppi and Royer-Carfagni, 2013).
For the assessment of glass in terms of strength and failure behaviour, the four-point bending setup provides an accurate means for testing. Moreover, it allows for obtaining the critical bending and tensile stress and fracture pattern especially for laminated glass samples. In this case, fractographic observations of the broken specimens indicate if the failure occurred on the surface or on the edge of the glass ply.
The current paper aims at evaluation of laminated glass samples with EVA, PVB and Ionoplast interlayers in terms of mechanical behaviour in four-point bending and validation of finite element model by test data.
Finite-Element Modelling
Laminated glass can be considered as a sandwich structure that consists of linear-elastic glass plies and a viscoelastic thermoplastic layer, which provides shear transfer between the glass plies. To determine the bending stress in laminated glass, well-established analysis techniques do not guarantee the real stress results or, in some cases, give results with large scatter. For highest design reliability, the Element Method (FEM) has been applied. The main advantages of using FEA is the ability to obtain the bending stress in every layer of a multi-layered laminate. The aim of the FE calculation was to verify the numerical results against the experimental test data and calculate the bending stresses in four and six glass plies laminates with EVA and PVB interlayers.
ABAQUS 3D Model
Four-point bending set-up of laminated glass samples was modelled in the commercial ABAQUS/CAE software. Due to the tests performed in experimental campaign, two FE models were created.
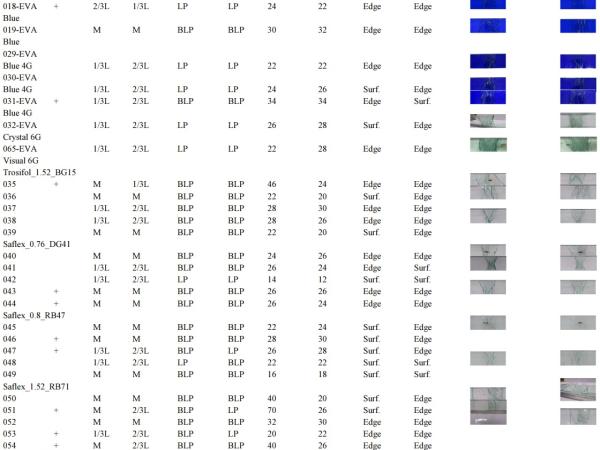
First, a model was created for two-ply (Fig. 1) laminates where the supports and loading rollers were defined as 3D analytical rigid parts with dimensions according to the test set-up. For laminated glass, 8-node continuum shell element SC8R were used. The elements look like three-dimensional continuum solid element; however, its kinematic and constitutive behaviour is similar to the conventional shell element (Hibbit et al., 2001). Moreover, the continuum shell elements have only displacement degrees of freedom. The glass and interlayer parts were assembled and tie constraints between them were created. The tie constraints are surface based and were used to tie together two surfaces for the whole duration of a simulation. Each node on the slave surface is constrained to have the same motion as the point on the master surface to which it is closest (Hibbit et al., 2001).
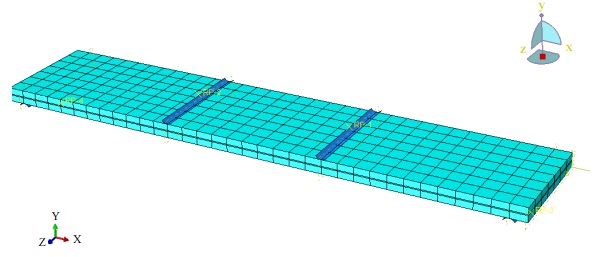
A second model was created for four and 6-ply (Fig. 2) laminates. Compared to the first model, additional load introduction details have been applied. In this model, the supports and load were created as 3D analytical rigid parts. Because of the movement during the test, a 3D solid element was applied for the loading rollers and metal loading detail and a continuum shell SC8R element for the laminated glass sample. The parts were assembled and interaction surface-to-surface contact applied. As in the first model, a tie constraint was used to model the bond between the glass and polymer interlayers. Between metal and glass surfaces, tangential behaviour contacts with a friction coefficient of 0.5 was applied.
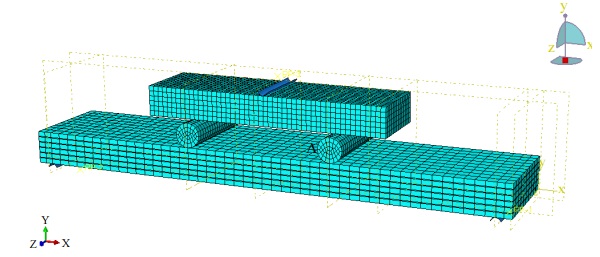
Since the real bending stress value is not known, a mesh convergence study was done and presented in Fig. 3.
Two different studies for mesh density have been done. The basic principle of mesh studies is to find the optimum element size that gives accurate results, moreover, the more DOFs in the model the better it can capture the structural behaviour. As shown in Fig. 3 the mesh density influences the stress results more than the displacement results. Since additional DOFs increase computation time, also a time convergence study has been done. According to the convergence study, elements with 15 mm size have been chosen and applied to the final models (Fig. 1 and 2).
Materials and Interlayer Influence on FE-Analysis
All materials (glass and interlayers) were modelled using elastic material model parameters. To evaluate bending stress values, mechanical properties for the materials were collected from the literature; otherwise, test evidences must support each material properties. The material properties for soda lime glass are defined as follows - Young’s modulus, Eglass = 70 GPa and Poisson’s ratio, υglass = 0.23 (EN 572-1, 2017)
The results of FEA simulations must correlate to the experimental data, however, one of the reasons for the results contradiction can be interlayer variable behaviour, which depends on temperature and load duration. Three mechanical properties that characterize the interlayer linear elastic zone are Young’s Modulus, Shear Modulus and Poisson’s Ratio. Moreover, according to Hooke’s Law, by increasing the elastic modulus also the shear modulus increases which means that shear transfer between glass plate and interlayer increases. It must be taken into consideration that interlayer behavior is temperature-dependent and mechanical properties must be defined according to the laboratory temperature.
In the literature, studies on PVB material have mainly focused on the elastic properties investigation at different temperatures and true stress-strain curve calculations (Santarsiero et al., 2016). Also, PVB interlayer producers offer data tables with interlayer mechanical properties which depend on temperature and load duration (Eastman Chemical Company, n.d.; Kuraray GmbH., n.d.). The following properties according to producer’s public data sheets are recommended values for FE analysis, however, in practice they are lower and must be verified by test evidences. In all simulations, which were done for this research, Poisson’s ratio for PVB material was a fixed value at 0.498 but Young’s Modulus was customized for each interlayer type and ranges from 2-90 MPa.
A limited number of studies have been reported on EVA interlayer material mechanical behaviour at different temperature and strain rate. Several authors’ (Serafinavičius et al., 2013; Weller et al., 2005) experimental investigations revealed that also EVA interlayer is time and temperature-dependent. Limitations of the studies (Castori and Speranzini, 2017; Serafinavičius et al., 2013) are type of EVA interlayer, authors focus mainly on evaluation of standard type of EVA material. However, range of EVA products is large and each type has considerable difference in mechanical properties. Currently, producers do not offer public data sheets for EVA material physical properties. For this reason, properties were taken from literature as EEVA = 10-20 MPa and υEVA = 0.32 (Castori and Speranzini, 2017; Czanderna and Pern, 1996; Pankhardt, 2008).
Analytical Calculation
In this article, a method for determining the effective thickness of laminated glass for analysis of stresses and deflection has been applied (prEN 16612, 2017). According to the following formulas (Equation 1, 2), effective thicknesses have been calculated and substituted into the standard engineering formulas for four-point bending test maximum stress and deflection approach:
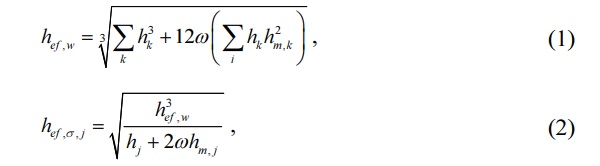
Where:
ω = Coefficient between 0 and 1 representing no shear transfer (0) and full shear transfer (1)
hk , hj = The thicknesses of the glass plies
hm,k, hm,j = The distances of the mid-plane of the glass plies k, j, respectively, from the mid-plane of the laminated glass
hef,σ,j = The effective thickness for calculating the stress of glass ply number j
hef,w = The effective thickness for calculating bending deflection
According to prEN 16612 (2017), the shear coefficient ω is defined for the interlayer. As mentioned before, EVA interlayer has not been discussed in standard, for this reason it can be defined by “Family 1” where ω takes values of 0 to 0.3. Calculation was done with the value 0.3 according to suggestions by Hána et al. (2018). Interlayers SaflexDG41 and SentryGlas® ionoplast are assumed to be in “Family 2” and ω - 0.7, PVB Sound 0.76 interlayer is “Family 0” and ω - 0. All other PVB interlayers are assumed to be in “Family 1” (standard PVB) and ω - 0.3.
Laminated glass samples have been tested in 4-point bending where the failure stress was calculated with Equation 3:

where, a – distance between loading and support point, F-maximal force, b-sample width, hef,σ,j - the laminate effective thickness for calculations of bending stress.
The maximum deflection is calculated according to Equation 4:

where, E-Elastic modulus of glass (70 GPa), I- moment of inertia (calculated according to Equation 5), l1 – distance between supports:

Experimental Investigation
Test Setup
Laminated glass specimens have been tested in 4- point bending in the laboratory of the Faculty of Engineering LTH at Lund University in Sweden. In the tests, a uniaxial tensile machine with the capacity of 100 kN was used. The distance between the supports and loading points was assumed constant for all samples (Fig. 4). The specimens were loaded with a constant displacement rate of 6 mm/min until failure of all glass plies. This displacement rate was chosen to achieve a constant stress rate within the load span of approximately 2 MPa/s. While surveying the literature for other experiments on glass using the four-point bending setup, it was found that a stress rate of approximately 2 MPa/s was most commonly chosen (Kinsella, 2018), moreover, a stress rate of 2 +/- 0.4 MPa/s is recommended in the standardized setup according to EN 1288-3:2000. Loading and cross-head displacement have been recorded throughout the tests.
As the samples have been made using thermoplastic interlayers, special attention was paid to the control of climate in the testing room. The tests were carried out at 25±1°C with the relative humidity of 44±1%. Measurements were collected during the tests and calculated as an average value.
For accurate longitudinal strain measurement in glass at high stress region, strain gauges LY 11-10/120 (Fig. 5) were bonded to the glass at the tension and compression side in the middle of the sample.
Test Specimens
The laminated glass specimen dimensions were 500 mm×100 mm, the values of an average specimen thickness and the number of tests is shown in Table 1.
All laminated glass samples were manufactured from annealed soda lime glass and industrially cut on cutting machines and with polished edges. Laminated glass specimens have been prepared according to interlayer production process.
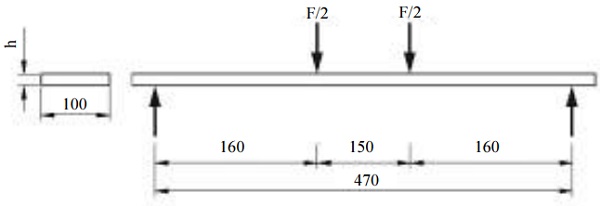

Table 1: Test samples overview
Results and Discussion
This section summarizes the experimental and numerical results. In the next paragraphs, samples test results, FEA and analytical results are discussed separately, including the measurements obtained from strain-gauges. For a better understanding, samples with additional marks 4G and 6G refer to the number of glass sheets in the specimen.
“Post-Breakage” Phase Observation
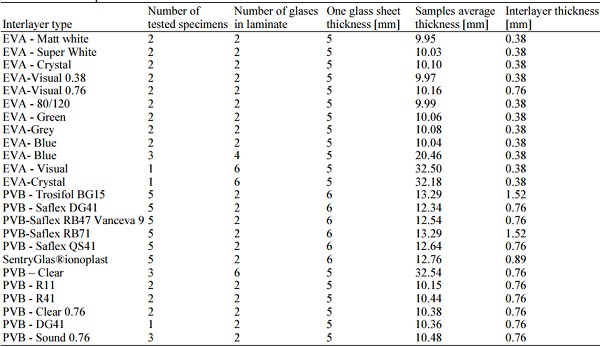
During experiments, two types of failure for the laminated glass specimens were observed (Fig. 6).
With the first type, both glasses collapse simultaneously under the load as a monolith glass and the curve is linear with one maximal load peak (Fig. 6 curve A). With the second type, first collapses the tensile side of the glass but compression side pane is still able to carry the load and two maximum load peaks or more can be seen in graph (Fig. 6 curve B). In this case, a so called “post-breakage” state can be observed which is also described in Delincé et al. (2008). The post-breakage state of laminated glass is defined as the state when one or more glass sheets are cracked and the broken glass pieces are still bonded to the interlayer. Delincé et al. (2008) Post breakage phenomena have to be analyzed especially for load bearing structures, because of the laminate’s ability to maintain integrity and carry the loads after collapse. There are several factors which affect laminate postbreakage behavior, for example, glass fragments size after breakage, interlayer properties, load duration, adhesion between interlayer and glass surface, etc.
In this research paper, the laminated glass “postbreaking” phase results are not discussed, however, Table 4 shows that for 55% of all samples this phase is observed. For further analytical calculations, the maximum force (Fmax) and the corresponding displacement (Dmax) values are used (Fig. 6).
Strain Gauge Measurements
Strain gauges were glued on the specimen’s upper and lower glass surfaces to determine the maximal longitudinal strain in the glass at failure. In general, the Young’s modulus of glass was assumed as Eglass = 70 GPa (EN 572-1, 2017; Pfaender, 1996) which allows, according to Hooke's Law, to calculate maximal bending stress in glass plies. The maximal normal stress results obtained from strain gauge measurements, FE analysis and analytically calculated results are presented in Table 3.
Table 2: Comparison of strain gauge measurements and FEA results
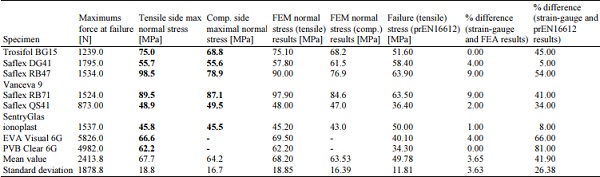
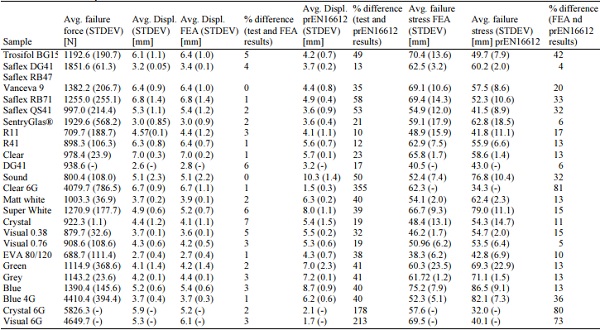
Table 3: Average value of failure force, displacement, failure stress, FEA results, analytical results and standard deviations for all series samples
Strain measurements is instrumented to provide data for comparison to finite element analysis (FEA) results and to validate the FE model. The percentage difference between strain gauge measurements at the bottom plate and FE analyses is 0-4%. An exception are the samples with Trosifol BG15 and Saflex RB47 interlayer for which the strain in the bottom glass ply is 9% and 25% higher, respectively, than in the top ply. However, the analytical approach gives results with a larger scattering, for two-layer laminates between 5- 54% and for six glass laminates between 66% and 81%. This disparity is explained by the implemented shear transfer coefficient ω that is too general and conservative, from the other hand, it serves also as a safety factor in engineering calculations.
From the test results it can be concluded that the stiffer the interlayer is, the more the plate behaves like a monolithic structure and the difference between the top and bottom strain measurements are smaller.
PVB Interlayer Samples
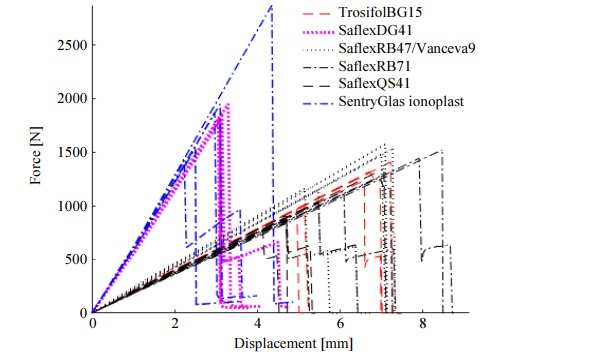
Table 3 presents a range of statistics including the average failure force for all tested samples with PVB and Ionoplast interlayer. Figure 7 compares the experimentally measured force-displacement curves for two glass laminates where the glass thickness is 6 mm and the PVB interlayer thickness is 0.76 mm and Ionoplast thickness is 0.89 mm.
There is a close agreement seen for the results in Figure 7 between samples with PVB Saflex DG41 and SentryGlas® Ionoplast interlayer. The highest average failure force (Table 3) was recorded for SentryGlas Ionoplast – 1929.6 N (SD 568.2) and Saflex DG41 – 1851.6 N (SD 61.3) where the corresponding average displacement was 3.0 mm (SD 0.85) and 3.2 mm (SD 0.05). Compared to specimens with Saflex DG41 and SentryGlas®, the average displacements are 50% lower for the Trosifol BG15, Saflex RB47&Vanceva 9, Saflex RB71, Saflex QS41 interlayers. The disparity between the results can be explained by interlayer properties, for example, PVB Saflex DG41 (ECC, 2015) and SentryGlas® Ionoplast (Kuraray GmbH, n.d.) interlayer is 100 times stiffer than conventional laminating materials at the same temperature and load duration.
The lowest load at failure was found for samples with Saflex QS41 interlayer – 997 N with SD 214.4. Specimens with BG15, RB47Vanceva9 and RB71 have equal results (Table 3).
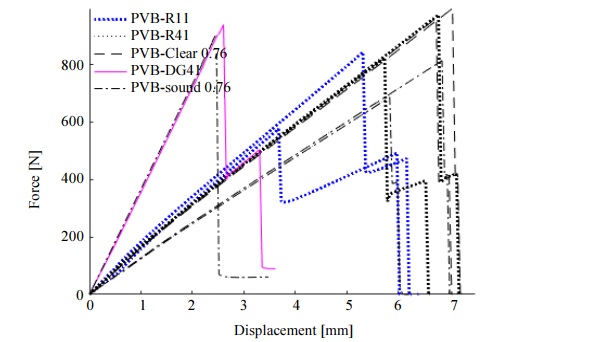
Figure 8 and Table 3 represent experimental results of two glass laminates, where 5 mm glass was used. A higher average force was sustained by samples with PVB Clear and PVB - DG41 interlayer respectively 978.4 N (SD 23.9) and 938.6 N. It must be mentioned that in this case there are only two observations per data sample available which limits the statistical significance, however, a rough estimate is conveyed for the mechanical behaviour under bending load.
Figure 9 illustrates the results of 6-ply glass laminates with PVB clear interlayer. The average failure force was determined as 4079.7 N (SD 786.5) and the corresponding displacement was 6.7 mm (SD 0.9). The figure also shows that the slope of the forcedisplacement curve is not linear which means that viscoelastic properties of the interlayer affect the results.
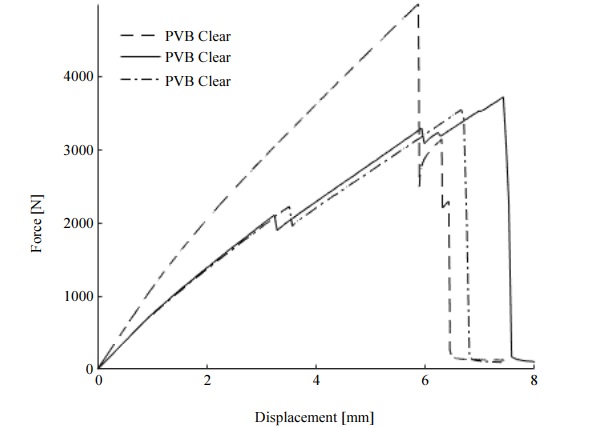
EVA Interlayer Samples
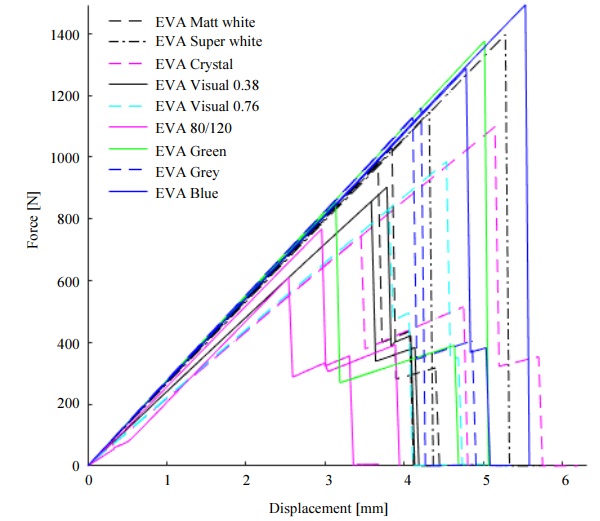
Figure 10 presents test results for two glass laminates samples with EVA interlayer. The thickness of the interlayer is 0.38 mm, except for samples with EVA Visual 0.76 mm film where the nominal thickness is 0.76 mm.
Figure 10 and Table 3 show that there is a significant difference between test results and the type of interlayer affects force and displacement results. It can be explained by the small number of specimens that do not provide for a complete statistical analysis. However, a disparity between the results also confirms the hypothesis that each EVA interlayer type has unique properties and must be evaluated for further research.
The lowest failure force is observed for samples with EVA - 80/120 interlayer - 767 N and 609 N. A significant difference is shown by two series samplesEVA – Crystal and EVA – Green where results are 746 N, 1098 N and 1375 N, 854 N, respectively.
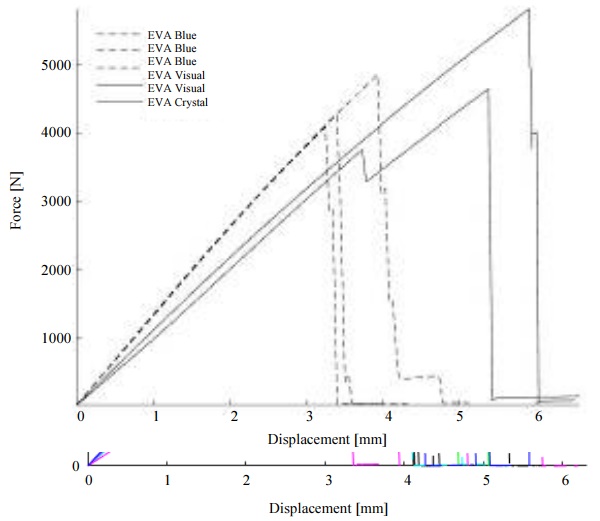
More complex behavior under bending load is illustrated by the test results (Fig. 11) of 4 and 6 glass laminates. The curves with dashed lines represent 4 glass plates with EVA – Blue interlayer but solid lines 6 glass laminate with EVA-Visual and EVA-Crystal interlayer.
From the results presented in Fig. 11 and Table 3 it can be concluded that the curves, compared to the samples with two glass plies (Fig. 10), do not show perfect linearity. This curvature can be explained by the effect of interlayer and its mechanical behavior during the loading process. Maximal force is at least 3 times higher, but the displacement retains the same values.
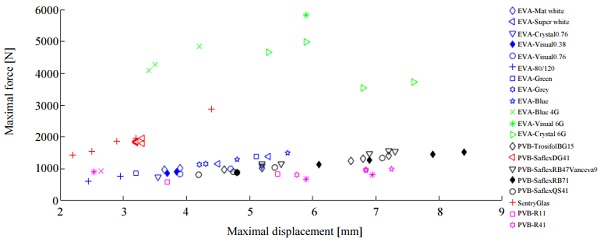
One of the glass engineering main questions are “what is the best interlayer for specific application?” To describe and evaluate the capacity of laminated glass with different interlayer’s resistance to deformation in elastic zone, all specimens test results were presented in one chart. In Fig. 12, the failure force is plotted against measured corresponding displacement for all specimens.
Some limitations of this research must be taken into consideration. First, the tests were conducted under laboratory conditions. As mentioned before, interlayer mechanical behavior affects temperature, for this reason, for structures, which deal with outdoor conditions; static calculations must be done with properties for those conditions. Second, it is difficult to explain such results based on the full information of EVA interlayers properties. Further investigation requires a full test cycle for determination of the exact ω value for all types of EVA.
However, the results in Fig. 12 highlight that specimens with EVA interlayer are competitive and give two times smaller displacement results than specimens with standard PVB interlayers, except for “stiff interlayers” (Saflex DG41 and SentryGlas®). Furthermore, the data shows a dispersion between one interlayer results. Even though the difference is small, it may have a significant impact on structural calculations.
Visual Inspection Results
The strength in glass material is stochastic in nature and depends on the existence of microcracks on the surface. The strength is governed by the stress-enhancing flaws that limit the practical strength to some 20-140 MPa for annealed glass (Regan, 2014). Glass material fracture, branching of cracks, fracture spread and failure origin are phenomena which are not unambiguously explained or predictable. One of the advantages with laminated glass is the possibility to evaluate the material fracture pattern after failure. Several authors tried to predict and analyze the glass fracture process. Veer and Rodichev (2012), the fracture pattern in water-jet cut glass is analyzed. The fracture patterns are divided into four categories; however, it is noted that according to research for glass with polished edge, only two types of fracture patterns are generally observed, namely, centre fractures and V-fractures.
Table 4 presents pictures with the glass material failure pattern and the determined fracture location and ratio of damaged area to whole sample plate area. For the understanding of Table 4, abbreviations have been introduced. The heading “fracture location” describes three types of location where cracks have been observed - Middle of sample (M) and at some part of span (1/3L, 2/3L), where L – full length of beam. Measurements were made from the outer edge of the sample. “Fracture area” describes position of fracture area - located Between Loading Points (BLP) or direct under Loading Roller (LP). In the case of 4- point bending test, the maximum bending moment is reached between the loading points. The “Area of cracks” was evaluated to determinate the area of material damaged by the load. A parameter is calculated corresponding to the ratio of crack to the whole surface area. After the test, all specimens were visually examined and the maximum dimensions of the crack area were measured, furthermore, the results were expressed as a percentage. In section, “type of fracture” are listed the type of failure origin, either edge or surface fracture.
As mentioned before, (Veer and Rodichev, 2012) described two type of fracture. In this research paper the centre crack is defined by a surface crack (Fig. 13 a) and the V-crack by an edge failure (Fig.13 b).
In the case of an edge failure, a “V” type crack occurs after breakage of the glass and extends from one point on the sheet edge. The second type is the surface failure with the crack starting from the glass surface when the glass breaks.
Table 5 gives information about the failure proportions of all tested samples. The first step in breakage analysis is determining the origin or location where the breakage occurred. In this case, the proportion of fracture location shows that in bottom plies 42% of cracks started at the middle on the specimen but in top plies 66% started under the loading points. This large percent can be explained by glass and metal roller interaction. According to (EN 1288-3, 2016), rubber sheets must be inserted between the glass specimen and metal, however, for full scale (360×1100 mm) specimens the rubber does not affect the result, but for smaller and thinner samples it can change the force-displacement curve.

Table 4: Samples failure mode and fracture patterns
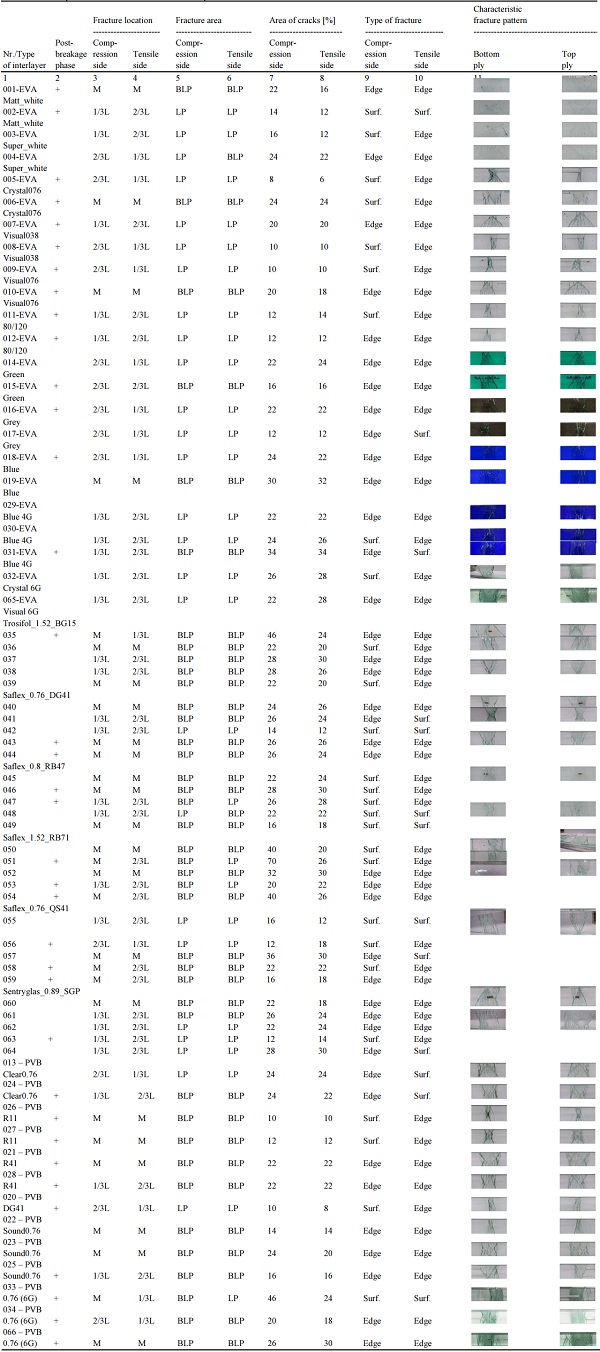
Table 5: Fracture location statistics
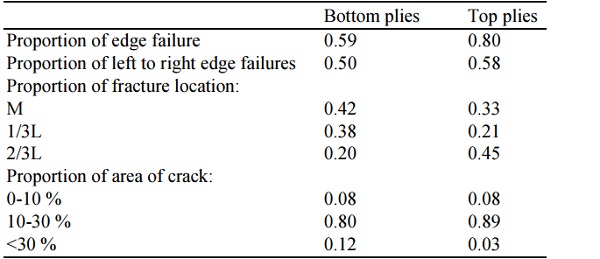
The proportion of edge failures shows that 59% of tensile side breakages were due to edge failures, but for the top plies it was 80%. Previous studies confirm that glass material breaks unpredictably, moreover, this result coincides with Veer and Rodichev (2012; 2011).
The ratio of crack area shows that under bending load 10-30% of the whole sample is damaged. This number is important for crack spread evaluation and for a determination of how large an influence the interlayer has in this process. From Table 4 it can be concluded that “crack area” is not dependent on the type of interlayer. All sample series exhibit high scattering of results and minimal repeatability.
One of most interesting observations is glass failure in shear (samples with Saflex_1.52_RB71 interlayer) or sheet separation. The pieces of glass were separated layer by layer, which is not a typical failure type. This type of failure can be explained by assumption that the glass surface had excellent adhesion with interlayer and under the load, the glass material could not withstand the high strength of the adhesive bond.
Summary and Conclusion
The current research paper shows experimental, analytical and numerical studies on two, four and six glass laminates with EVA and PVB interlayers; a total of 66 samples were tested.
For accurate longitudinal strain measurement in glass at high stress levels, the strain gauges were glued on the glass at the tension and compression side in the middle of the sample. Four-point bending tests of laminated glass were modelled in the software ABAQUS/CAE. With the models it was possible to predict the maximal force and displacements in the tests and to evaluate the bending stresses. All FE models were validated by test data.
Analytical calculated displacement results are at least 10-58% higher compared to FE analysis and test results. According to current research, the conclusion can be drawn that by using the finite element method it is possible to accurately simulate the mechanical behaviour in 4-point bending with very high result correlation with differences less than 5%. These 5% errors can be explained by interlayer variable behaviour, which depends on temperature and load duration.
The results, which were identified by the experiments, confirms that EVA can be treated in the modelling approximately equally to PVB. It must be mentioned that the conclusions hold under laboratory conditions and further research needs to be carried out to verify the claim for temperature ranges and environments outside of the laboratory conditions.
Multi-layered laminates and 55% of two glass laminates test results allow for an evaluation of the so-called “post-breakage” phenomena. The specimens showed the same behavior – first collapsed the bottom glass (tension side) and then other glass layers.
A glass fracture pattern investigation confirms that there appears to be no preference for the edge failures to occur from the left or right side of the beams. This indicates that the test setup was proper and that the loading of the specimens occurred without significant tilting which would otherwise probably promote breakages from either the left or the right side. More than half of the failures originated with the edge. In addition, more than half of the failures occurred outside the load span stressing the fact that glass fracture is stochastic in nature and challenging to predict. The ratio of cracked area to specimen surface area is not dependent on the type of interlayer.
Acknowledgement
This research was supported by Erasmus+ programme. Authors express their gratitude to PRESS GLASS SA company and RI.SE for providing the specimens.
Author’s Contributions
Liene Sable: Performed tests, evaluated the results, analysing and interpreting the results, contributed in drafting the article.
David Kinsella: Contributed in analysing and interpreting the results, contributed in drafting the article.
Marcin Kozłowski: Performed tests and contributed in drafting the article, reviewed the article.
Ethics
All authors have been personally and actively involved in substantive work leading to the manuscript. The authors declare that there are not conflicts of interest.
References
ASTM 1300, 2010. Standard practice for determining load resistance of glass in buildings. ASTM Int.
Castori, G. and E. Speranzini, 2017. Structural analysis of failure behavior of laminated glass. Composites Part B: Eng., 125: 89-99. DOI: 10.1016/J.COMPOSITESB.2017.05.062
Czanderna, A.W. and F.J. Pern, 1996. Encapsulation of PV modules using ethylene vinyl acetate copolymer as a pottant: A critical review. Solar Energy Mater. Solar Cells, 43: 101-181. DOI: 0.1016/0927-0248(95)00150-6
Delincé, D., D. Callewaert, J. Belis and R. Van Impe, 2008. Post-breakage behaviour of laminated glass in structural applications. Challenging Glass, 3: 459-467.
Eastman Chemical Company. (n.d.). Vanceva ® Polyvinyl Butyral Interlayer Product Technical Data.
ECC, 2015. Architectural Technical applications center storage conditions: Saflex ® DG Mechanical and Physical Properties. 1–5. Eastman Chemical Company.
Eekhout, M. and W. Sluis, 2014. Glass Elevator Shaft for the Mauritshuis-The Hague. In: Challenging Glass 4 and COST Action TU0905 Final Conference, Louter, B.B. and Lebet (Eds.), CRC Press, ISBN-10: 1138001643, pp: 123-588.
El Amrani, A., A. Mahrane, F.Y. Moussa and Y. Boukennous, 2007. Solar module fabrication. Int. J. Photoenergy, 2007: 1-5. DOI: 10.1155/2007/27610
EN 1288-3, 2016. Glass in building-Determination of the bending strength of glass - Part 3. Test With Specimen Supported Two Points (Four Point Bending).
EN 572-1, 2017. Glass in building - Basic soda-lime silicate glass products - Part 1. Definitions General Physical Mechanical Properties.
Galuppi, L. and G. Royer-Carfagni, 2012. The effective thickness of laminated glass plates. J. Mechanics Mater. Structures, 7: 375-400. DOI: 10.2140/JOMMS.2012.7.375
Galuppi, L. and G. Royer-Carfagni, 2013. The effective thickness of laminated glass: Inconsistency of the formulation in a proposal of EN-standards. Composites Part B: Eng., 55: 109-118. DOI: 10.1016/J.COMPOSITESB.2013.05.025
Grohmann, M., 2014. Transparency. Proceedings of the Challenging Glass 4 and COST Action TU0905 Final Conference, (TFC’ 14).
Hána, T., M. Eliášová and Z. Sokol, 2018. Structural performance of double laminated glass panels with EVA and PVB interlayer in four-point bending tests. Int. J. Structural Glass Adv. Mater. Res., 2: 164-177.
DOI: 10.3844/SGAMRSP.2018.164.177
Hibbit, D., B. Karlsson and P. Sorensen, 2001. ABAQUS/CAE User’ s Manual. Ver. 6.10.1. ABAQUS Inc.
Kinsella, D., 2018. Survey of experimental data on the strength of annealed float glass panes in the asreceived condition tested in an ambient atmosphere. Technical report TVSM-7166. Division of Structural Mechanics, Lund University.
Kuraray GmbH, (n.d.) 2019. Physical properties of sentryglas ® and butacite®.
Kuraray GmbH. (n.d.). Trosifol® TROSIFOLTM – World of Iinterlayers.
Lamon, J., 2016. Brittle Fracture and Damage of Brittle Materials and Composites. 1st Edn., Elsevier Science, ISBN-10: 008101161X, pp: 296.
Pankhardt, K., 2008. Investigation on load bearing capacity of glass panes. Periodica Polytechnica Civil Eng., 52: 73-82. DOI: 10.3311/PP.CI.2008-2.03
Pfaender, H.G., 1996. Schott Guide to Glass. 2nd Edn., Springer Science and Business Media, ISBN-10: 9401105170, pp: 224.
prEN 16612, 2017. Glass in building - determination of the lateral load resistance of glass panes by calculation.
prEN16613, 2017. Glass in building-Laminated glass and laminated safety glass-Determination of interlayer mechanical properties.
Raynaud, J., 2014. Smooth Free-form Glass Skins. In: Challenging Glass 4 and COST Action TU0905 Final Conference, Belis, L.B. and Lebet (Eds.), ISBN-10: 978-1-138-00164-0, pp: 57-65.
Regan, C.O., 2014. Structural Use of Glass in Buildings. 1st Edn., Institution of Structural Engineers, ISBN10: 1874266514, pp: 168.
Sandén, B., 2015. Which interlayer for which glazing application? Glass Performance Days, 5: 153-155.
Santarsiero, M., C. Louter and A. Nussbaumer, 2016.
The mechanical behaviour of SentryGlas® ionomer and TSSA silicon bulk materials at different temperatures and strain rates under uniaxial tensile stress state. Glass Structures Eng., 1: 395-415. DOI: 10.1007/S40940-016-0018-1
Serafinavičius, T., J.P. Lebet, C. Louter, T. Lenkimas and A. Kuranovas, 2013. Long-term laminated glass four point bending test with PVB, EVA and SG interlayers at different temperatures. Procedia Eng., 57: 996-1004. DOI: 10.1016/J.PROENG.2013.04.126
Veer, F.A. and Y.M. Rodichev, 2012. The strength of water jet cut glass. Glass Performa. Days, 20: 434-438.
Veer, F.A. and Y.M. Rodichev, 2011. The structural strength of glass: Hidden damage. Strength Mater., 43: 302-315. DOI: 10.1007/S11223-011-9298-5
Weller, B., J. Wünsch and K. Härth, 2005. Experimental study on different interlayer materials for laminated glass. Glass Process. Days, 5: 120-123.