Article Information
- Digital Object Identifier (DOI): 10.47982/cgc.8.451
- This article is part of the Challenging Glass Conference Proceedings, Volume 8, 2022, Belis, Bos & Louter (Eds.)
- Published by Challenging Glass, on behalf of the author(s), at Stichting OpenAccess Platforms
- This article is licensed under a Creative Commons Attribution 4.0 International License (CC BY 4.0)
- Copyright © 2022 with the author(s)
Authors:
- Xing-er Wang - Shanghai Jiao Tong University
- Jian Yang - Shanghai Jiao Tong University
- Shennan Peng
- Yige Wang - Shanghai Jiao Tong University
- Xiaonan Hou - Lancaster University
Abstract
The bridging behavior between fragments is one vital factor in the post-fracture stage of glass laminates. A particle-based discrete element model was developed in this work to simulate the bridging behavior of fractured glass laminates. The model was based on the calibration of hyperelastic PVB material properties using soft-bond model and further validated with the experimental data as well as the observations from through-crack-tensile tests. In order to investigate the bridging performance of fractured glass laminates with multiple fragments under uniaxial tension, three factors encompassing the crack aligning, fragment number and adhesion conditions were considered to perform a parametric study.
The results give an exploratory application of the developed discrete element models in the estimation of the post-fracture behaviors. It is found that the smaller fragment size can diminish the tension-stiffening effect in the non-aligned case which might generate an enhancing ratio of initial modulus up to nearly 3.6. The non-aligned cracks can also lead to a very high strength if the adhesion ability can be guaranteed. However, the delamination of fragments is expected to control the post-fracture strength of fractured glass laminates with PVB interlayer.
1. Introduction
Laminated glass (LG) has been increasingly used to make load bearing members in the construction industry because of its unique transparency and enhanced structural performance due to the updated use of novel interlayers (Hänig & Weller, 2020). Polyvinyl butyral (PVB), ionoplast polymer (e.g. SentryGlas, SG) (Biolzi et al., 2020; Chen et al., 2020) might be the most frequently adopted interlayers for structural glass. In addition to improving the combined performance under static action, e.g., out-of -plane wind load, interlayers can also guarantee a higher post-fracture ability. Post-fracture performance of structural glass is of significance as the glass layers still present high vulnerability to various types of loads such as blast load (Angelides et al., 2021). The related reports on the post-fracture behaviors of structural glass can see an evident rise in the last few years.
Interlayers and their adhesion ability to glass yield vital influences on the post-fracture ability of laminated glass by different means. Biolzi et al. (Biolzi et al., 2018) tested the in-plane load bearing capacity of LG beam using DG41 and DG41/polycarbonate (PC) interlayers. The tension-stiffening (TS) effect was found to improve the post-fracture stiffness via connecting the shattered glass fragments. A thin PC layer can also reduce the negative effect from creeping behaviour of DG41 interlayer and thus benefit the long-term flexural capacity of fractured LG beam. A theoretical analysis on the post-fracture behaviour of laminated tempered glass under in-plane and out-of -plane load (Galuppi & Royer-Carfagni, 2018) shows that the TS effect depends on the size of glass fragments and debonded area between fragments and interlayers. A typical scenario demanding the post-fracture performance of LG members is blast event (Angelides et al., 2019; Del Linz et al., 2017), in which the membrane effect of fractured LG panels can fully use the resistance of both interlayer and adhesion.
Numerical method, as a vital tool to investigate the insightful failure mechanism of glass laminates, is hence expected to capture various key features when adopted to simulate the post-fracture behaviour. Those features encompass the significant discontinuity of glass fracturing, interlayer tearing and large deformation of fractured glass members (Wang et al., 2021). Finite element (FE) method has been very popular in modelling the failure process of structural materials including LG materials (D’Ambrosio et al., 2019). A recent attempt using realistic fracture pattern reconstructed by a quadtree mesh withprismatic polyhedral elements (Saputra et al., 2021) was conducted by Saputra et al.(2021).
However, FE method still presents great difficulties in simulating the entire failure process with all above features, in particular, when contact detection and computation are demanded in the cases such as assessing the number and velocity of flying debonded fragments in the blast or the gradual collapse of glass structure. A promising update is to combine FE with polygonal discrete element (DE) technique (Wang et al., 2020). In this work, particle-based DE method is primarily concerned, as it might provide more universal solution and flexibility based on DE framework. As well known, the calibration of microscale bond parameters in DE model might be sophisticated particularly when the nonlinearity or other complex characteristics of materials are invoked (Rorato et al., 2021).
In this work, a particle-based DE model was developed to simulate the post-fracture behaviour of glass laminates. The hyperelastic property of PVB material was calibrated as well as its adhesion to glass. It is followed by developing a model of fractured glass laminates taking through-crack-tensile (TCT) tests as example. The numerical results were validated with the experimental data and observations. Fractured glass laminates with multiple fragments under tension (i.e., MTCT tests) were subsequently simulated to give an exploratory application of the developed models. The influence due to fragment number, cracks aligning, adhesion on the bridging behaviour of fractured glass laminated was examined.
2. Development of DE model
2.1. Calibration of interlayer properties
The commonly used interlayers in structural glass are PVB and SG interlayers. Preliminary trials show that the currently available contact models in the software package PFC2D have difficulties in simulating certain elasto-plastic behaviours, in particular, when the material (e.g., SG) which yields at small strain and has its final failure at a very large strain. In contrast, a soft bond model can well describe the hyperelastic behaviour of PVB interlayer. Thus, PVB was adopted in this work. It has been found that PVB presents significant strain rate dependency which should be carefully considered in the dynamic simulation. This work concentrates on the static behaviour of fractured glass laminates and therefore omits such features.
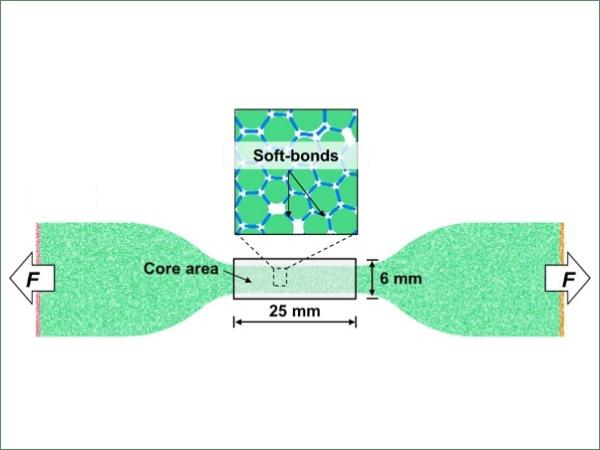
Uniaxial tensile (UT) tests were firstly performed on the PVB specimens at room temperature to provide the experimental results for validation. Three dogbone shaped specimens with a core area of 25 mm x 6 mm (Fig. 1(a)) were tested to guarantee the repeatability. The tested strain rate was set as 0.01 s-1. The DE models with identical geometry of UT specimen were then developed to calibrate the microscopic bond parameters of PVB material. The expansive particle packing method which gradually expanded the particle sizes to compact until achieving the defined porosity was used. A particle radius range from 0.1 mm to 0.13 mm was determined. As PVB has large elongation at failure and low elastic modulus, a soft bond model enabling the softening behaviour of material was used to connect the particles. The frictional behaviour between particles was allowed in this model before the shear strength completely declines to zero (Fig. 1(b)).
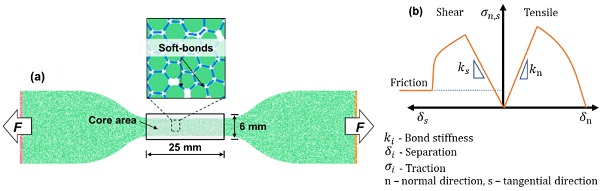
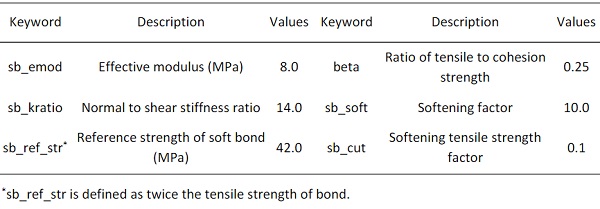
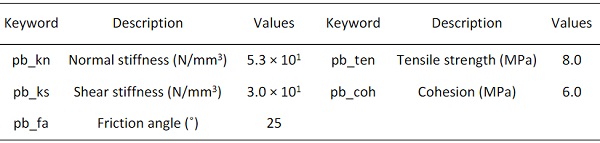
Several key parameters were selected and adjusted to determine an appropriate parameter set, which was able to reproduce satisfactory results of stress strain relationship including the nonlinearity and large strain features of PVB under tension. As there are many bond parameters that might affect the tensile property, only effective modulus, stiffness ratio, reference strength, bond strength ratio were used to perform the calibration as well as two parameters related to softening behaviour. It is noted that the effective modulus refers to a combined property which couples the normal and tangential bond stiffness. The determined parameters were given in Table 1 after trials-and-errors calibration.
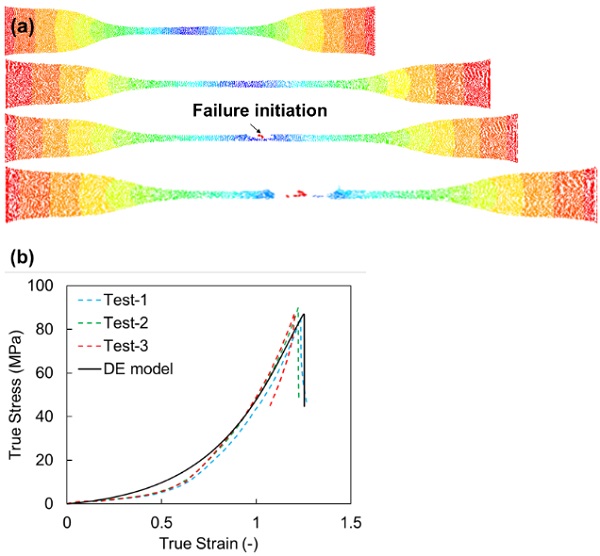
The deformation process till the final failure of numerical UT specimen was shown in Fig. 2(a). A large deformation at failure can be clearly observed. As the numerical model commonly demands an accurate input of true stress-strain behaviour of materials, Fig. 2(b) shows the comparison between the numerical results and experimental data of true stress-strain curves. The hyperelastic growth of the constitutive law can be well reproduced in the calibrated DE model, whilst the numerical result has high consistency with the testing data.
The results and observation indicate that the calibrated parameters can give reliable prediction on modelling the hyperelastic behaviour of PVB interlayer.However, it is worth noting that many more important influencing factors such as temperature, moisture, strain rate can result in significant variation of the material properties. In those cases, the calibrated model cannot well describe the concerned features. More microscale parameters or other bond models (e.g., Edinburgh-Elasto-Plastic-Adhesive contact model) can be used or re-programmed to present more applicable calibration.
Table 1: Calibrated microscopic bond parameters of PVB interlayer
2.2. DE model of TCT test
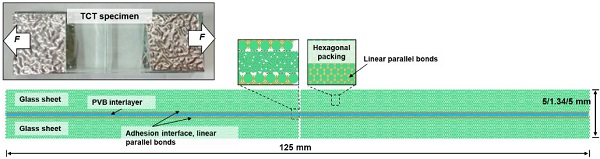
A typical load case of structural glass which demands its post fracture capacity is the blast load. The membrane action on the fractured LG member under blast is highly related to the tensile properties of the laminated fragments and interlayers. Thus, most of current works focus on the post-fracture tensile behavior of LG. A popular experimental approach to investigate the post-fracture ability of fractured LG is the TCT test (Fourton et al., 2020), which tests a double layered LG specimen with one aligned transverse crack on each glass sheet. In this work, TCT tests on three PVB LG specimens were conducted to validate the numerical results. The mean true thickness of PVB interlayer after lamination is around 1.34 mm. Each float glass sheet has a thickness of 5 mm. The dimension of TCT specimen is 125 mm x 40 mm.
The DE model of TCT specimen adopted a hexagonal packing strategy for the glass sheet and an expansive particle packing method for PVB interlayer. The theoretical solutions to approximate the elastic property of isotropic material using hexagonal packing can be found in (Ismail et al., 2015). The equations for contact stiffness are given as:
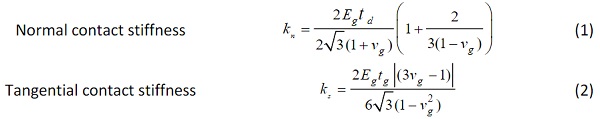
where Eg is the elastic modulus, vg is the Poisson’s ratio and tg denotes the particle thickness. The parallel bond model (Ma & Huang, 2018) which neglects the softening stage of soft-bond model was used to bond the hexagonal packed glass particles. The parallel bonds can be seen as many elastic springs distributed over the contacts between particles. Once the spring strength is reached, bond will have brittle failure. The tensile bond strength was set to be the fracture strength (45 MPa) of float glass. As float glass is adequate to avoid glass fracture in a TCT test on PVB LG, the bond strength is not a key variable.
The experimental observation shows that PVB LG has a gradual delamination process without seeing the cohesive fractures of glass. Therefore, parallel bond model was also assigned to the interface between glass and PVB. Combined with the current report and our lab tests (Pelfrene et al., 2015; Samieian et al., 2019), the fracture energy via delamination is determined as 1 N/mm in tangential direction and 0.6 N/mm in normal direction. The delamination strength is 8.0 MPa. The calibrated bond parameters for glass to PVB adhesion are given in Table 2. The developed DE model of TCT specimen is shown in Fig. 3.
Table 2: Calibrated microscopic bond parameters of glass-PVB adhesion
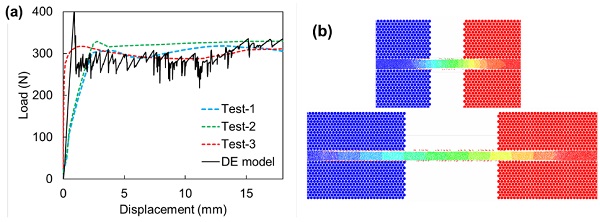
A constant load speed of 0.2 m/s was employed to the right edge of numerical TCT specimen. The comparison of the load-displacement curves from the numerical and experimental results is shown in Fig. 4(a). It is found that the numerical result can obtain highly close results to the testing data in the steady state delamination stage. The steady state delamination force is around 300 N. It is worth noting that the stiffness before the delamination initiation from the numerical prediction approaches that of Test-3, which is higher than those of other tests.
Through additional study on the adhesion property of glass to PVB interface, a higher bond strength in the normal direction might be the predominant factor of yielding a higher stiffness. The stronger normal adhesion results in more difficulties of the decohesion and the subsequent stretch of interlayer (Fig. 4(b)). However, it will not greatly affect the steady state delamination process. Despite of the oscillation due to the dynamic bond failure in DE simulation, the comparison shows that the developed DE model is adequate to give accurate prediction on the TCT tests.
3. DE modelling of MTCT tests
3.1. Modelling configurations
TCT test refers to an ideal unit of fractured glass laminate which has the aligned cracks and large glass fragments. The realistic fracture pattern of glass commonly has unaligned crack pattern in different glass sheets, which is found to present tension stiffening (TS) effect by the adhesion to fragments. TS effect can improve the interlayer stiffness via an alternative stress path through the fragments. In addition to the cracks aligning, the fragment size also significantly affects the post-fracture behaviour. Thus, the fragment size, the cracks aligning, adhesion condition were treated as the investigated variables to examine the associated influences on the response of the MTCT tests, which refer to the TCT tests with multiple fragments and indicates the bridging behaviors of realistic fractured laminates.
The geometrical details of the MTCT models were identical to those in TCT tests, except that the interlayer thickness was 0.76 mm. The fragment size was roughly estimated by the fragment number N50, which was the minimum number limit of tempered glass fragments in an area of 50 mm x 50 mm. A range of N50 from 10 to 150 with an increment of 35 was selected to develop the DE models of fractured glass laminates. Both aligned cracks and non-aligned cracks were considered. In the laminates with non-aligned cracks, the cracks in the bottom glass sheet was assumed to locate at the centre of each glass fragment in the upper sheet. Two adhesion conditions, calibrated glass-PVB adhesion in Table 2 and share-nodes adhesion, were employed. The latter adhesion indicates that there is no relative separation between glass and connected PVB particles. It should be noted that the initial debonded area at the edges of each glass fragments, which can also weaken the post-fracture stiffness, was not considered in current work.
3.2. Parametric study on bridging behaviors
The right edge of MTCT specimens were subjected to a tensile load speed of 0.2 m/s. As the stretch of interlayer and the delamination were the major concern in a tensile test, the compressive contact detection between glass fragments was disabled to reduce the computation cost. The displacement limit was set as 50 mm. The numerical observations of MTCT tests at the final displacement limit were shown in Fig. 5. From Fig. 5(a) and (b), it is seen that with smaller fragment number the debonded area of non-aligned case is larger than the other case. For example, more debonded fragments can be found when N50 is 45 and 80 in Fig. 5(b), whereas the difference of the debonded area tends to diminish as N50 is 115 and 150 between aligned and non-aligned cases.
This indicates a decreasing trend of TS effect in non-aligned case with greater fragment number, i.e. smaller fragments lead to a shorter transferring path of stress inside the fragment. From Fig. 5(c) and (d), it is found that with a perfect adhesion condition, the aligned cracks will facilitate the accumulation of the tensile strain within interlayer, which finally yields the tearing of interlayer and the failure of MTCT specimens. In the non-aligned case, only several local cracks can be seen in the interlayer which cannot generate the tearing of interlayer. The local cracks vanish when the fragment number further increases to a higher value than 45.

The load displacement results from DE simulation of MTCT tests were transformed into the relationships of stress-train results by adopting the equivalent stress which omited the thickness of glass sheets. The equivalent stress-strain curves were collected and shown in Fig. 6. From Fig. 6(a) and (b), it can be seen that by introducing the adhesion properties between glass and PVB interlayer, the gradual delamination of fragments will result in a similar developing stage to the steady state delamination in TCT tests. A plateau of stress can be found in this stage.
Although the cases with N50of 115 and 150 does not reach the stress plateau at the final step, from the growing trend of stress-strain results it can still be inferred that they will see the stress plateau near the stress magnitude at the final step. Comparing the stress at the plateau in the aligned and non-aligned cases, non-aligned cracks can greatly improve the steady state delamination stress with small fragment number. The stress increase in the non-aligned case will gradually decline as the fragment number rises.
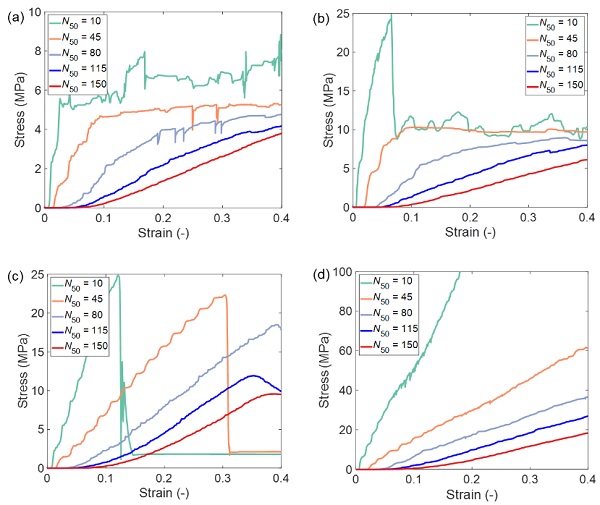
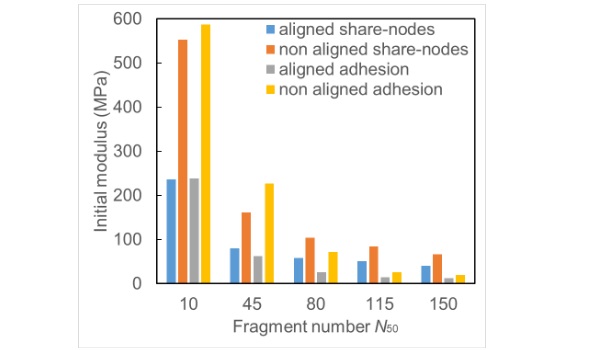
From Fig. 6(c) and (d), as the failure is resulted from the local tearing of interlayer in the aligned case, the stress-strain results show a brittle failure mode. Smaller fragments are seen to yield lower failure strength. It can also be seen that the post-fracture strength can reach a very high value if the adhesion can be guaranteed. The initial modulus which indicates the stiffness of the fractured glass laminates from each case was calculated and shown in Fig. 7. The modulus difference between the case with aligned shared-nodes and that with adhesion is found to be negligible when the fragment number is small. The difference will gradually increase once the fragment number rises whilst the case with aligned adhesion finally presents a very low modulus.
Similar finding can also be identified in the cases with non-aligned cracks. The initial modulus from the case with non-aligned share-nodes is smaller than that from the case with non-aligned adhesion when the fragment number is 10 or 45. The opposite trend can be seen when the fragment number keeps increasing. By comparing the result from the case with aligned adhesion and that with non-aligned adhesion, the increase of fragment number can greatly reduce the TS effect which might generate a modulus up to around 3.6 times the value from the aligned case. Overall, the significant influences due to the fragment size can be clearly found from the results of initial modulus.
4. Conclusion
A particle-based discrete element model was developed to simulate the bridging behaviour of fractured glass laminates with PVB interlayer. The hyperelasticity and large strain behaviour of PVB material was modelled using soft-bond model. The glass-PVB adhesion and glass materials were described with parallel bond model. The developed model was validated with the experimental data and observation of through-crack-tensile tests. It is found that the proposed model can well reproduce the steady state delamination process and the stretch of interlayer.
It is followed by a parametric study on examining the influences due to the crack aligning, fragment number and adhesion conditions on the bridging ability of glass laminates with multiple fragments. The results reveal that with larger fragment number, i.e. smaller fragment size, the tension stiffening effect in laminates with non-aligned cracks contributes less on improving the stiffness, which might yield an equivalent modulus up to 3.6 times that of laminate with aligned cracks. A perfect adhesion with non-aligned cracks can generate very high strength, however, the adhesion failure controls the post-fracture strength of fractured glass laminates with PVB interlayer.
Acknowledgements
This study was funded by the National Natural Science Foundation of China [Grant No. 52078293,51908352] and the Shanghai Science and Technology Innovation Action Plan [Grant No. 20dz1201301].
References
Angelides, S. C., Talbot, J. P., & Overend, M. (2019). The effects of high strain-rate and in-plane restraint on quasi-statically loaded laminated glass: a theoretical study with applications to blast enhancement. Glass Struct. Eng., 4(3), 403-420. https://doi.org/10.1007/s40940-019-00107-4
Angelides, S. C., Talbot, J. P., & Overend, M. (2021). High strain-rate effects from blast loads on laminated glass: An experimental investigation of the post-fracture bending moment capacity based on time–temperature mapping of interlayer yield stress. Constr. Build. Mater., 273, 121658. https://doi.org/10.1016/j.conbuildmat.2020.121658
Biolzi, L., Cattaneo, S., Orlando, M., Piscitelli, L. R., & Spinelli, P. (2018). Post-failure behavior of laminated glass beams using different interlayers. Compos. Struct., 202, 578-589. https://doi.org/10.1016/j.compstruct.2018.03.009
Biolzi, L., Cattaneo, S., Orlando, M., Piscitelli, L. R., & Spinelli, P. (2020). Constitutive relationships of different interlayer materials for laminated glass. Compos. Struct., 244, 112221. https://doi.org/10.1016/j.compstruct.2020.112221
Chen, S., Lu, Y., Zhang, Y., & Shao, X. (2020). Experimental and analytical study on uniaxial tensile property of ionomer interlayer at different temperatures and strain rates. Constr. Build. Mater., 262, 120058. https://doi.org/10.1016/j.conbuildmat.2020.120058
D’Ambrosio, G., Galuppi, L., & Royer-Carfagni, G. (2019). A simple model for the post-breakage response of laminated glass under in-plane loading. Compos. Struct., 230, 111426. https://doi.org/10.1016/j.compstruct.2019.111426
Del Linz, P., Hooper, P. A., Arora, H., Wang, Y., Smith, D., Blackman, B. R. K., & Dear, J. P. (2017). Delamination properties of laminated glass windows subject to blast loading. Int. J. Impact Eng., 105, 39-53. https://doi.org/10.1016/j.ijimpeng.2016.05.015
Fourton, P., Piroird, K., Ciccotti, M., & Barthel, E. (2020). Adhesion rupture in laminated glass: influence of adhesion on the energy dissipation mechanisms. Glass Struct. Eng., 5(3), 397-410. https://doi.org/10.1007/s40940-020-00136-4
Galuppi, L., & Royer-Carfagni, G. (2018). The post-breakage response of laminated heat-treated glass under in plane and out of plane loading. Compos B Eng, 147, 227-239. https://doi.org/10.1016/j.compositesb.2018.04.005
Hänig, J., & Weller, B. (2020). Load-bearing behaviour of innovative lightweight glass–plastic-composite panels. Glass Struct. Eng., 5(1), 83-97. https://doi.org/10.1007/s40940-019-00106-5
Ismail, Y., Sheng, Y., Yang, D., & Ye, J. (2015). Discrete element modelling of unidirectional fibre-reinforced polymers under transverse tension. Compos B Eng, 73, 118-125. https://doi.org/https://doi.org/10.1016/j.compositesb.2014.12.024
Ma, Y., & Huang, H. (2018). DEM analysis of failure mechanisms in the intact Brazilian test. Int. J. Rock Mech. Min. Sci., 102, 109-119. https://doi.org/https://doi.org/10.1016/j.ijrmms.2017.11.010
Pelfrene, J., Van Dam, S., & Van Paepegem, W. (2015). Numerical analysis of the peel test for characterisation of interfacial debonding in laminated glass. Int. J. Adhes. Adhes., 62, 146-153.
Rorato, R., Arroyo, M., Gens, A., Andò, E., & Viggiani, G. (2021). Image-based calibration of rolling resistance in discrete element models of sand. Comput. Geotech., 131, 103929. https://doi.org/https://doi.org/10.1016/j.compgeo.2020.103929
Samieian, M. A., Cormie, D., Smith, D., Wholey, W., Blackman, B. R., Dear, J. P., & Hooper, P. A. (2019). On the bonding between glass and PVB in laminated glass. Eng. Fract. Mech., 214, 504-519.
Saputra, A., Behnke, R., Xing, W., Song, C., Schneider, J., & Kaliske, M. (2021). Numerical representation of fracture patterns and post-fracture load-bearing performance of thermally prestressed glass with polymer foil. Eng. Struct., 226, 111318. https://doi.org/https://doi.org/10.1016/j.engstruct.2020.111318
Wang, X.-E., Yang, J., Huang, X., Wang, F., & Zhu, Y. (2021). Voronoi-FDEM concept for modelling post-fracture response of progressively damaged structural glass. Eng Comput. https://doi.org/10.1007/s00366-021-01318-6
Wang, X.-E., Yang, J., Pan, Z., Wang, F., Meng, Y., & Zhu, Y. (2020). Exploratory investigation into the post-fracture model of laminated tempered glass using combined Voronoi-FDEM approach. Int. J. Mech. Sci., 105989. https://doi.org/10.1016/j.ijmecsci.2020.105989