Buckling behaviour of laminated glass panel in compression

Authors: Mohd Khairul Kamarudin, Nurul Hariyanti Mohd Rais, Mustafasanie M. Yusoff and Gerard A.R. Parke

Source: MATEC Web Conf., 258 (2019) 05010

DOI: https://doi.org/10.1051/matecconf/201925805010

Abstract

There is a significant increase in the application of laminated glass panel in the modern and innovative construction industry. Glass element is frequently used as a structural component because of its aesthetic and allows abundance of daylight shining in through in which leads to energy saving. The glazing consists of two thin glass plates bonded together by a thin core material called polyvinyl-butyral (PVB). A laminated glass panel is typically brittle and slender, thus frequently subjected to buckling. This paper focuses on the load-carrying behaviour of laminated glass panel supported merely along four edges subjected to compressive force. A 1 m x 1 m laminated glass panel with glass plies of 8 mm thick and the interlayer thickness of 1.52 mm is modeled and analyzed through nonlinear static analysis by using ABAQUS finite element (FE) analysis software.

The behaviour of the laminated glass panel under buckling and post-buckling analysis was presented. Analytical approach by Zenkert's formulation based on the theory of sandwich is utilized to validate the technique used to build the FE model of the glass panel. Essentially, the critical buckling load and the load-displacement relationship are in a good agreement with the analytical formulation and the empirical study respectively. In addition, the significant effect of the interlayer and the slenderness aspect of the panel are also studied. This involves parametric analysis of the configuration of the different interlayer stiffness and the aspect ratio length to width (a/b) of the glass panel. It was found that the rate of decrement of buckling load is indirectly proportionate to the rate of increment of (a/b) ratio. This study also shows that the buckling load of a laminated glass panel depended very much on the slenderness aspect of the structure. 

1 Introduction

The demand of monolithic or laminated glass element in modern application such as in construction of innovative and futuristic architecture showed a great increment in the building constructions especially in Europe. It offers interesting and unique opportunities in the realization of innovative architecture of modern buildings. One of the great innovations of structural glass can be seen at Zhanjiajie Glass Bridge, China that spans 430 m long bridging between two hills [1]. During the past decade, the use of this material has been increased because of the development of new techniques for glass manufacturing and the escalation trend of computational structural analysis through finite element method.

As the pacing of glass industries developments stride ahead, it can be seen that glasses are not only used as window panels, it is now can also be used in structural element of the building. Laminated glass (LG) is normally consisting of two or more layers of glass bonded with plastic interlayers such as Polyvinyl Butyral (PVB). When glass shatters, a post-breakage behavior is prevailed due to the fragments that stick to the plastic interlayer. Interlayer keeps the fractured glass together in which increases safety. If one glass pane breaks, the remaining layers can continue to carry the applied load and desirably inhibit a sudden collapse.

Generally, glass is a brittle material that is weak in tension because of its non-crystalline molecular structure. Due to the characteristic of high slenderness ratios, LG element is frequently subjected to buckling phenomena. It has a high compressive strength but with limited tensile resistance. The bonded layer of thermoplastic viscous polymer is intrinsically able to provide ductility and enhanced post breakage behavior. Thin cross section of LG panel justifies the element is mainly adopted for member in tension or bending. The load carrying capacity of LG panel or beam strongly depends on the mechanical properties of interlayer, the presence and the amplitude of possible imperfection as well as the externals loads. Engineers are advised to do finite element simulation or simplified calculation to determine buckling load of LG [2]. Initially, the studies on the critical load of LG are always comprised between two well-known monolithic and full layered arrangements. 

The load carrying behaviour of laminated safety glass in compression depends strongly on the temperature and the load duration due to the shear connection with the viscoelastic PVB interlayer [3]. Investigations showed that this shear connection, which can be simplified on the safe side with an elastic approach, might only be taken into account for short term loading like wind and impact. The load carrying behaviour can be described using elastic sandwich theory or known as Zenkert’s formulation. For further simplification the cross section of a laminated safety glass structural element can be modelled as a monolithic cross section with an effective thickness.

Studies on the ability of PVB interlayer to transfer shear force between glass plies in LG beams subjected to uniaxial bending has been presented [4]. The results substantiate that glass is the constitutive material prone to reach its ultimate limit, which is the tensile strength, while PVB does not exceed its elastic limit. This research has proved that the actual behavior of LG beam may range from 50 to 100% of the wellbonded plates of glass plus pieces of polymer. Thus, LG beams may behave far from monolithic. The sensitivity analysis developed by using analytical model shows that the buckling strength strongly depends on the thickness of the interlayers, the environment temperature and the load duration (rate). 

Compressive test of glass panel and glass column, and also bending test of monolithic and laminated glass panels are presented and discussed [5]. The main variable considered were slenderness of panels and the shape of the cross section of columns. The brittle failure was observed due to a buckling phenomenon. The specimen buckled, visual crack were formed in the middle and at the end of the specimen; and delamination occurred. The experiment proved that the failure load decreased with the increment of height of the panel. Increasing slenderness by 25% caused 16% reduction in failure load. An analytical formulation is proposed for the estimation of the buckling resistance of flat LG panels under in-plane compression or shear [6].

Two different design approaches are taken into account and compared: the first one directly derives from the theory of sandwich panels, whereas the second one is based on the approximate concept of equivalent thickness. Because of their characteristic high slenderness, LG panels subjected to in-plane compression or shear can be affected by stability problems. The performed numerical simulations shows that sophisticated 3D models frequently present convergence problems, especially if used to analyze LG panels in which the shear connection between glass sheets is approximately zero. Comprehensive characterization of the compressive response of LG is still lacking in sources and no theoretical prediction of the critical load are available in the design standard, therefore, no scientific result warns about laminated glass in compression.

Structure engineer and designer always avoid laminated glass panel in compression because of the general assumption that the LG element is too slender. Laminated glass beam and panel under axial compressive load are frequently subjected to stability problem.  Numerous studies has been conducted, focused on buckling response of glass panel subjected to in -plane shear providing a good and very informative data.  But the knowledge on compressed laminated glass panel behavior is still limited and with constrained application. Due to the brittle behavior and randomness of strength, glass structure requires a design process in which is different from the approach used in traditional building materials. There was no realistic way to determine the actual reliability with the safety factor principle regarding to the laminated glass panel.

In addition, many studies have focused on the compressive load of beam and flexuraltorsional of the beam, but only few studies are currently available about compressive behavior of the panel. Through this reasoning, this study would have presented the results of the behavior of laminated glass panel under compressive load by using modelling 3D ABAQUS/CAE software. Realistic buckling verification of laminated glass panel should be performed by means of research study concerning the resistance, serviceability and durability of such brittle element. Therefore, the approach in this study is to propose the behavior of laminated glass panel under compressive forces. 

Hence, the main objectives of this study are to evaluate the performance of buckling behavior of laminated glass panel subjected to compressive load. A parametric study on the buckling behavior of laminated glass panel having different stiffness of interlayer and geometrical properties is carried out and eventually the performance of post-buckling behavior of laminated glass panel is evaluated. 

2 Development of the FE model

Finite element method (FEM) was used with tools ABAQUS/CAE 6.14 software in order to study the behavior of laminated glass panel. A specific attention is given on the buckling response of laminated glass panel under compressive force. This study provides a numerical assessment in evaluation of the critical buckling load of laminated glass panel. In the first model that relate to the first objective, a laminated glass panel with dimension 1.0m (length) x 1.0m (width) with thickness of pane 8mm (glass 1) /1.52mm (interlayer) /8mm (glass 2) was built up in the ABAQUS. The interlayer used in this study is PVB-interlayer. In-plane compression force was introduced in the model in the form of uniform distributed pressure acting on the upper and lower surface of the model and the buckling behavior of laminated glass panel is determined. Prior to this numerical study, analytical approach by Zenkert’s formulation based on sandwich theory was carried out to validate the model.

Non-linear analysis would be carried out in order to investigate the post buckling behavior of the laminated glass panel. This procedure will be achieved by using Static, Risk Method. An initial imperfection would be introduced in the model defined as a linear superposition of buckling eigenvalue obtained from the previous buckling analysis with a specified imperfection parameter. 

2.1 Structural model

2.1.1 Models for buckling and post-buckling analysis

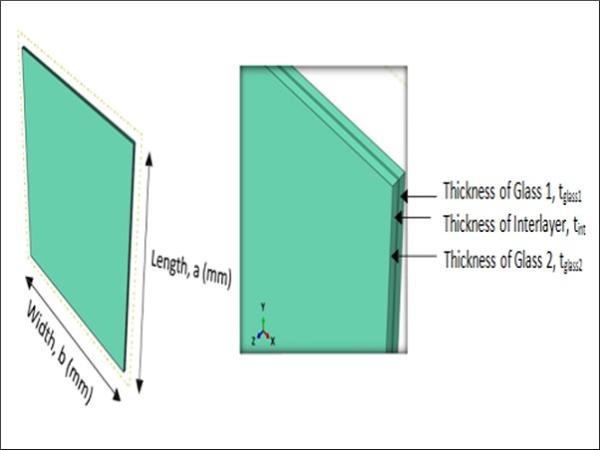
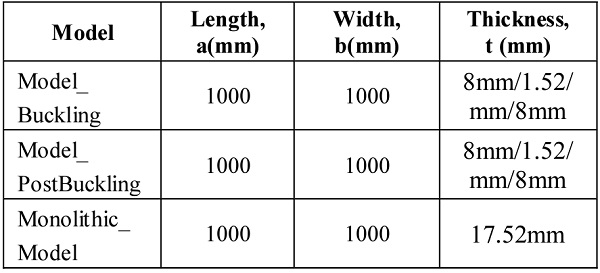
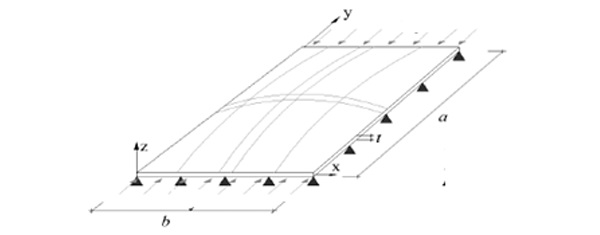
The laminated glass panel models were built up as shown in Fig. 1. The laminated glass panel model was built up as a 3D deformable solid part FE model which consisted of glass thickness tglass1 = tglass2 = 8mm and PVB interlayer thickness tint = 1.52mm. The geometrical properties of model for both buckling and post buckling analysis are presented in Table 1. 

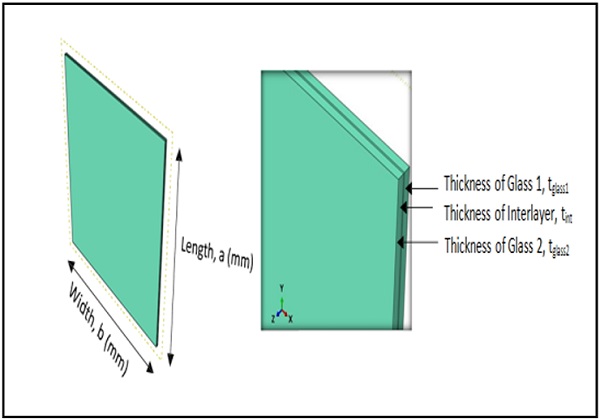
Table 1. Geometrical properties for buckling and post-buckling analysis 

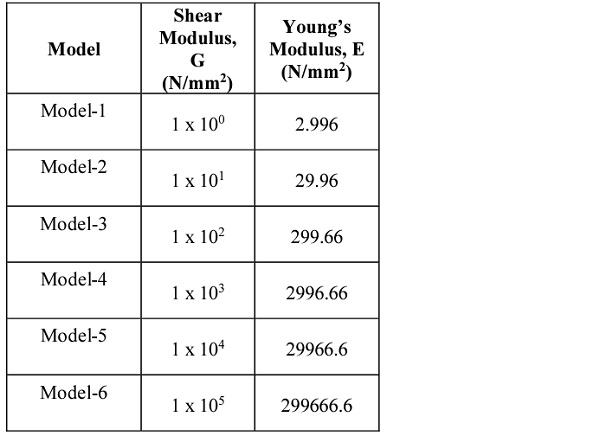
2.1.2 Models for analysis on the effect of different interlayer stiffness

By using constant geometrical properties of laminated glass panel (Length, a =1m, Width, b =1m, Thickness tglass1/tinterlayer/tglass2 = 8mm/1.52mm/8mm), the effect of variety stiffness of interlayer was investigated as tabulated in Table 2. 

Table 2. Geometrical properties for buckling and post-buckling analysis of different interlayer stiffness 

2.1.3 Models for analysis on the effect of different geometrical properties

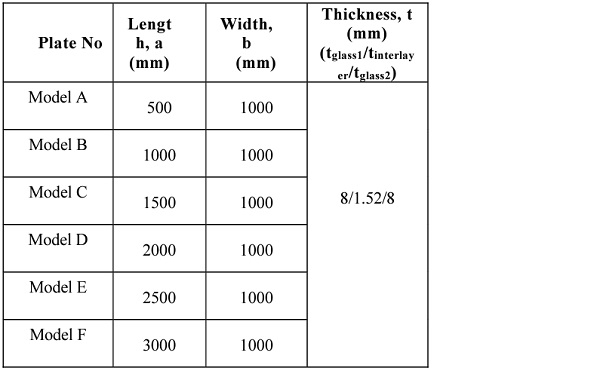
By using constant material properties of laminated glass panel, a parametric study on the effect of different geometrical properties of laminated glass panel to critical buckling load was investigated as tabulated in Table 3.

Table 3.  Geometrical properties used in analysis of the effect of different geometrical properties

The laminated glass panel model was built up as a 3D deformable solid part FE model which consisted of glass thickness; tglass1= tglass2 = 8mm and PVB interlayer thickness tint = 1.52mm. Both glass and interlayer (PVB) were created as a continuum shell and have material properties that act as homogenous materials. All models in this study were created by using linear continuum element with full integration in form of 3D + 8 node element (SC8R - 8 node quadrilateral in-plane general-purpose continuum shell, reduce integration with hourglass control, finite membrane strains). Continuum (solid) element was applied to the element because it can be used for a large variety of problem types. The continuum elements represent three-dimensional blocks of materials that can be connected to other elements on all of its faces, making it possible to create almost any structure.

Each of the nodes is having three translation degrees of freedom. In reduced integration, the element uses one integration point in each direction, and thus only a single integration point is used for the linear element.  In addition, hourglass stiffness was added in the element to limit the propagation of hourglass pattern (element possess no stiffness and strain energy are not monitored) in the mesh and to generate an acceptable result. During the development of the model, the laminated glass panel was modeled as being fully connected to each other at the corner and by assuming that there was an interaction between the surfaces. This modeling approach was achieved by making a datum and cut section through the panel so that the panel is separated into three different portions. With this approach, all sections were perfectly connected to each other and the different sections could be assigned different materials properties. 

2.2 Material properties

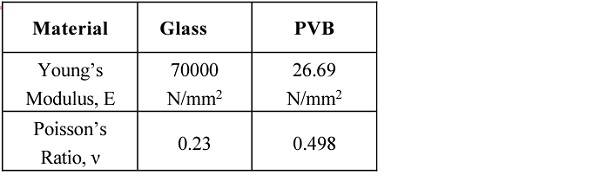
Glass is an isotropic material and when loaded and unloaded, it will respond perfectly as linear behavior. Glass is indeed a strong material, and at the same time very brittle and breaks easily. Material properties were nitially chosen in accordance with the previous study [6] as shown in Table 4. 

Table 4.  Material properties 

2.3 Loading and solution control

A simply supported laminated glass panel was modeled in the ABAQUS to evaluate the buckling analysis. The analysis was conducted in three steps. The first step is an initial displacement with static general procedure- linear analysis, the second was a perturbation-buckling procedure and the third one was Static Risk method-post buckling procedure. Analysis was conducted for both with and without nonlinear geometrical effect that takes into account the same boundary condition and load. Geometrical nonlinear occurs at the magnitude of the displacement that affects the structure of the response. It is generally caused by the following three situations: large deflection or large rotation; sudden flip; initial stress or load rigidity. In this analysis, the definition of geometric nonlinear problem is relatively used by using *STEP option and PERTURBATION parameters for buckling procedure.

It means that the change of geometry is taken into account that caused the buckle shape to form.  It is about a change in geometry where it significantly effects load deformation treatment. The conditions for the laminated glass panel were simply supported along four edges. Along the four edges, the translational degrees of freedom in z-directions (U3) as well as rotational degrees of freedom in 1, 2, 3 directions (θ1, θ2, θ3) were restrained to be zero. The four edges of the model were free to move along x-direction and y- direction as the longitudinal direction was subjected to displacement. Since the load applied in the y-direction only at top and bottom part of the model, the x–direction are assumed to have no displacement and reaction. The simplified presentation of boundary conditions is shown in Fig. 2 and Fig. 3.

In-plane compression was introduced in the model in the form of uniformly distributed pressure with magnitude P= 1 kN/mm2 acting on the upper and lower surface of the 3D element. This condition is used in all methods of analysis including the linear perturbation for buckling analysis and also the Static Risk for post-buckling analysis. In order to investigate the buckling behavior of laminated glass panel, a linear analysis was carried out. Linear analysis means that there is a linear relationship between the applied load and the response of the element in term of displacement. The load-displacement curve would be plotted to study the behavior of this element under compression. The linear response of the structure to the load cases can be found by multiplying the new vector of load by the inverted stiffness matrix. In this analysis, the *STEP option and PERTURBATION parameters for buckling procedure were used. This analysis was also used when conducting the parametric study on the effect of stiffness interlayer and the effect of geometrical properties of laminated glass panels.

A non-linear analysis was carried out in order to investigate the post-buckling behavior of this element by using Riks Method. The Riks method is a provided step analysis tool in ABAQUS to solve post-buckling problem in an unstable state of condition. Non-linear analysis using Riks method is suitable for post-buckling, or collapse of certain types of structures, materials, or loading conditions, where linear or eigenvalue method will become inadequate or incapable.

2.4 Sensitivity analysis

Sensitivity analysis in this study is used to obtain the optimum mesh density so that a good accuracy result without using excessive computer time will be achieved. In the model, it is very important to find a sufficiently accurate mesh for the element since the convergence of simulation and the accuracy of result would be seriously highlighted. There were 8 number of mesh sizes used to indicate when convergence is achieved and how far the value varies from theoretical studies. In this study, critical buckling load, Pcr for a simple monolithic glass panel with dimensions 1m x 1m x 0.008m (length x width x thickness) glass plate is analyzed by using the ABAQUS software with several values of mesh size. The result of the analysis is then compared to the theoretical value. The accuracy can be obtained directly related to the finite element mesh density that has been used. From the 8 numbers of mesh size used in the analysis, one would be selected that has a very small different mesh size percentage from the theoretical analysis which is 0.10 x 0.10. This mesh size is then used in this study. This process of mesh size selection is a key step in validating any finite element model and ensuring validity and reliability in the software, models and results. 

3 Analysis results and interpretation  

3.1 Verification of FE model

Analytical approach by Zenkert’s formulation based on sandwich theory was carried out to validate the FE models. In this procedure, the equations are based on the equation (1) to equation (3). The different between analytical and FE analysis are discussed in the next section. Based on the Zenkert’s formulation theory, the critical load of laminated glass panel is given by:

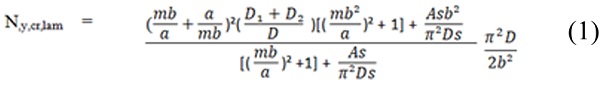
Critical load is comprised between two well-known, monolithic (Eq. 2) and full layered (Eq. 3) respectively are as below: 

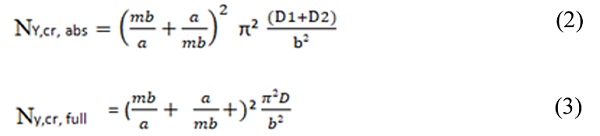
3.2 Buckling behavior of laminated glass panel

The buckling load of laminated glass panel was determined by FE analysis in ABAQUS. In this particular case, the laminated glass panel dimension is of 1000mm x 1000mm with thickness 8mm/1.52mm/8mm having shear modulus, Gint of 10 N/mm2. The comparison result between the FE analysis, the analytical formulation and the previous study in [6] is tabulated in Table 5. 

Table 5. Critical buckling load results of laminated glass panel,Ny,cr,lam

3.3 Parametric study

3.3.1 Effect of different stiffness of interlayer

The effect of stiffness of interlayer on the value of critical buckling load Ny,cr,lam are proposed for a laminated glass panel having dimension 1.0m x 1.0m with thickness 8mm/1.52mm/8mm. Depending on the shear modulus of interlayer, Gint of the material, the critical buckling load of the laminated glass panel is always comprised with well- known limit value monolithic, Ny,cr,abs and full layered, Ny,cr,full. PVB is a viscoelastic material and it is time – temperature dependent. Because of the assumption was made for this study that the interlayer PVB is assumed to behave in elastic, therefore the shear strength of interlayer should be converted into modulus of elasticity in order to perform the analysis. 

From Eq. 3, the values of critical bucking load for full layered, Ny,cr,full or assumed as full layered glass panel is 1306.34N. This is well known condition where full layered of glass achieved its maximum critical load at the stiffer interla yer. In addition, the critical buckling load Ny,cr,abs from Eq. 2 or assumed to use soft stiffness interlayer is 249kN. This means that it is the least value of critical buckling load, the laminated glass panel will sustain by using soft/weak inter layer. Finding these two values is an important aspect in the analysis, since the material is used to bond together the two glass sheets and to determine the limitation of critical buckling load and effect of stiffness of interlayer to the behavior of laminated glass panel. The analytical results are then compared.

The interlayer has a large relative impact on the stability of laminated glass panel, which can be seen when comparing the results from the graph in Fig. 4. Based on the graph, it is shown that increasing the shear modulus of interlayer will increase the critical buckling load of the laminated glass panel. The trend of the graph shows that the critical buckling load increases slightly at the first 1N/mm2 to 1000N/mm2 of stiffness interlayer. The load increase gradually when interlayer, Gint is greater than 1000N/mm2 until it achieves the value of critical buckling load of full layered limit, N,y,cr,full. 

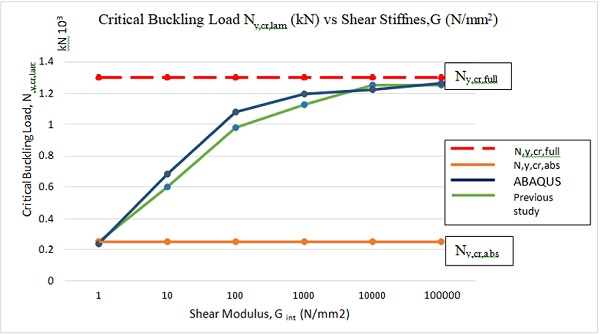
Table 6 shows the bucking loads that were also increase from 237.85 kN to 1261.72kN. As shown in Fig. 4, Ny,cr,full represents the stiffest interlayer where Gint > 10000N/mm2, whereas Ny,cr,abs shows the connection between glass sheets is too soft, Gint< 1N/mm2.

3.3.2 Effect of different geometrical aspect ratio of length, a to width (a/b ratio)

Panel with different geometrical properties are used extensively due to design requirements. Thus, the buckling response of laminated glass panel with its length to the width ratio must be fully understood in structural design. In this parametric study, several dimensions of laminated glass panel were tested. The length, a changed whereas the width, b was kept constant. In this study, six aspect ratios were evaluated. The panels and their corresponding results of buckling loads are shown in Fig. 5. 

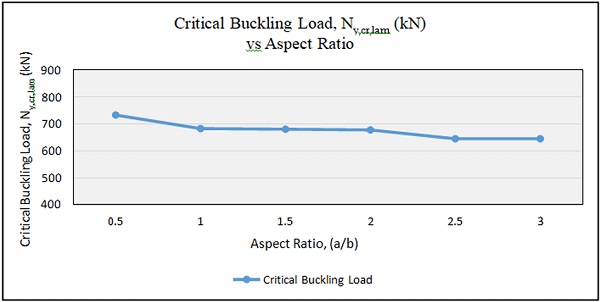
It can be seen that the buckling load gradually decreases with the increment of aspect ratio but the rate of decrement was not uniform.  It is observed that the buckling load was maximum for aspect ratio of 0.5 (N y,cr,lam  =732kN) and minimum for aspect ratio of  3.0 (N y,cr,lam =644.21kN). When the aspect ratio changed from 0.5 to 1.0, the reduction in buckling load was around 7%. The reduction value of critical buckling load seems to be small for aspect ratio 1.0 to 2.0 at about 0.76%. There were also reductions of buckling load about 4.77% between the aspect ratio of 2.0 to 3.0. From the graph, it is observed that the pattern of the buckling load was that it decreases with the increment of aspect ratio. 

3.4 Post-buckling analysis of laminated glass panel

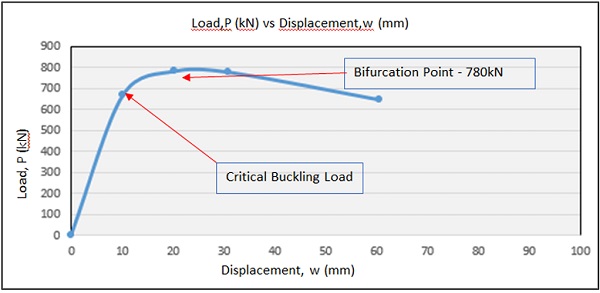
The post buckling analysis also concerns the typical load, P (kN) versus transversal displacement, w (mm) relationship characterizing the panel response of in-plane compressed laminated glass panel as shown in Fig.6.  Post buckling behavior of nonlinear model shows that the panel cannot increase its strength beyond the bifurcation point because the zero stiffness after buckling had occurred.

3.5 Discussion

The critical buckling load from FE, Zenkert’s formulation and previous study shows a good agreement. Though the sandwich theory formulation by Zenkert’s formulation shows a conservative value compared to the others, however it was found to be useful to evaluate the critical buckling load of the laminated glass panel.  When comparing between monolithic glass panel with laminated glass panel with similar geometrical and material properties of glass, in term of critical buckling load, it is very clear that the strength of laminated glass panel is higher compared to the monolithic glass panel. This is because of the two thin glass plates bonded together by thin core material called as interlayer that produces high impact of resistance. According to [7], laminated glass panel holds the concept of if one of the pane breaks, the remaining will continue to carry the load. The scattered glass pieces can stick to the interlayer thus; sustain the initial shape and the buckling resistance of the panel. 

A parametric study on the effect of stiffness of interlayer proved that the laminated glass panel strongly depends on the stiffness of the interlayer. Increasing the stiffness of interlayer will increase the buckling load of the element, until it reached the condition where the element reached it maximum critical buckling load before it breaks. The soft interlayer will give the lower strength. More stiff interlayer indicates that the interlayer hold both glass pane tightly, thus reduce the possibility of shearing effect that could result the instability of the panel. Stiffer interlayer found to be effective in structural design material. Stiffer interlayer can also store more energy and can support much load compared to the soft interlayer. Because of this reason, it reveals that the stiffness of interlayer gives effect on the strength of element. 

The strength of laminated glass panel also depends on the geometrical properties of the element. The slender the element, the lesser will be the buckling resistance. This also happen in all type of element especially column. Therefore, the knowledge on this geometrical effect is very important when designing the laminated glass panel as a structural element because the slenderness ratio of the panel will be used to classify the panel type. The study reveal that the higher the slenderness of the element, the more possibility it susceptible to failure. For short panel, it would fail by cracking on the edges first before it shatters.

It is known that studying in a realistic manner the behavior of laminated glass panel under compressive load especially in the estimation of critical buckling load does not constitute a useful criterion to define its actual ultimate strength, since the panel due to the post buckling effect could be able to sustain greater load than critical buckling. Therefore, analysis non-linear were done with ABAQUS software through **STATIC RIKS. The load is acting in the ideal state (upper and bottom part of model). From the result shows that the laminated glass panel cannot increase its strength beyond the bifurcation point because it has zero stiffness after buckling occurred. The result also reveals that the load in post buckling is higher than the buckling load analysis. The result shows bifurcation point is 780 kN. This is very important behavior on how far for the panel able to carry loads before its collapses.

4 Conclusions

A simplified but accurate formulation by Zenkert’s sandwich theory is used for the verification of the laminated glass panel. Comparison between FE and analytical study are presented to validate the accuracy of the numerical analysis. From the FE analysis, the following conclusions are made: 

1. It is proven that the critical buckling load of laminated glass panel for dimension 1m x 1m with thickness 8mm/1.52mm/8mm is Ny,cr,lam= 682.53kN. The critical buckling load of laminated glass panel was higher compared to the monolithic glass panel with similar dimension (Ncr=278.27kN). The study concludes that the application of laminated glass panel could increase 59.22% of the critical buckling load of the panel. The study also proved that the panel buckled and the increment of the load increases the displacement until it reached the critical buckling. There was a good correlation of critical buckling load between the FE and the previous study.  
2. It was seen that the interlayer stiffness affected the critical buckling load. When the stiffness increases, the buckling load increases until it achieved the maximum critical load, N,y,cr,lam. Critical buckling load for very soft interlayer Gint<1 N/mm2 was 237.85kN, whereas the critical buckling load for very stiff interlayer Gint>10,000N/mm2 was 1261.72kN.   Both of these values almost similar to the analytical approach result from Zenkert’s formulation. It was noted that the aspect ratio length, a to width, b (a/b) ratio affected the critical buckling load. The buckling load decreases as the aspect ratio (a/b) increases. The rate of decrement of buckling load was not uniform with the rate of increase of (a/b) ratio. The reduction of load was varies from 0.76% to 7%. The study revealed that the buckling load of a laminated glass panel depended very much in the slenderness of the structure.
3. The post buckling response of laminated glass panel and becomes unstable. The laminated glass panel did not increase its strength beyond the bifurcation point because it has zero stiffness after buckling occurred. The result also reveals that the load in post buckling was higher than the buckling load analysis. The result shows bifurcation point was 780kN with maximum displacement. 

References

1. Dotan, H, ‘Zhangjiajie Grand Canyon Glass Bridge’, Challenging Glass 5 – Conference on Architectural and Structural Applications of Glass, Belis, Bos & Louter (Eds.), Ghent University, 1-10. (2016)
2. preEN 16612: Glass in Building - Determination of load resistance of glass pane by calculation and testing.
3. Luible, A & Crisinel, M 2004, ‘Buckling Strength of Glass Element in Compression’, Structural Engineering International Journal, 14, 120-125 (2004)
4. Foraboschi, P, ‘Behavior and Failure Strength of Laminated Glass Beams’, Journal of Engineering Mechanics, 133, No. 12, 1290-1301 (2009)
5. Aiello, S et al, ‘Compressive Behaviour of Laminated Structural Glass Member’, Engineering Structures 33, pp. 3402–3408 (2011)
6. Amadio, C & Bedon, C, ‘Buckling of Laminated Glass Panel under in Plane Compression or Shear’, Engineering Structures 36, 185–197 (2012)
7. Fors, C ‘Mechanical Propeties of Interlayer in a Lamianted Glass’, Unpublished master dissertation, Department of Structural Mechanic, Lund University, Lund. (2014)