Detailed Modeling of Flat Plate Solar Collector with Vacuum Glazing

Authors: Viacheslav Shemelin and Tomas Matuska

Academic Editor: Stoian Petrescu

Source: Hindawi | https://doi.org/10.1155/2017/1587592

Abstract

A theoretical analysis of flat plate solar collectors with a vacuum glazing is presented. Different configurations of the collector have been investigated by a detailed theoretical model based on a combined external and internal energy balance of the absorber. Performance characteristics for vacuum flat plate collector alternatives have been derived. Subsequently, annual energy gains have been evaluated for a selected variant and compared with state-of-the-art vacuum tube collectors. The results of modeling indicate that, in the case of using advanced vacuum glazing with optimized low-emissivity coating (emissivity 0.20, solar transmittance 0.85), it is possible to achieve efficiency parameters similar to or even better than vacuum tube collectors. The design presented in this paper can be considered promising for the extension of the applicability range of FPC and could be used in applications, which require low-to-medium temperature level.

1. Introduction

The thermal use of solar energy for the production of heat from sunlight is one of the oldest energy transformation methods. This technology has been known and—sometimes even unconsciously—used for ages. It has been rediscovered and used again over the last 45 years. Today, it is ready for application, but after this short growth time, there is a large potential for development in this field, especially in the field of solar collectors.

As of now, the most widely used solar collector type in Europe is a solar flat plate collector (FPC). Simple structure, high optical efficiency, low cost, and safe operation are its main features. However, FPC is generally designed for a low temperature level between 40°C and 60°C, which is mostly the case for the domestic hot water system. Any shifts to a higher temperature level could bring the extension of the applicability range of FPC. Hence, efforts aimed to improve the performance of flat plate solar collectors are ongoing. The performance of a flat plate solar collector is largely influenced by the thermal losses from the absorber to the ambient via the transparent cover. One way to reduce this heat loss is to reduce the natural convection heat transfer in the space between the absorber and the cover by its partitioning with the use of additional glass pane, plastic film, or transparent insulation materials (TIM). Another way to reduce this heat loss is to use gas with lower thermal conductivity rather than air or by evacuating the space.

Veinberg BP and Veinberg VB [1] investigated the use of “deep narrow meshes” as solar transparent honeycomb insulation. Further, Hollands [2] presented the theoretical performance characteristics of a cellular honeycomb as a convection suppression device placed between the absorber and the outer glass cover of the FPC. Tabor [3] presented a brief picture of the cellular honeycomb construction, indicating that a successful use of honeycomb insulation requires a material with better physical properties and manufacturing techniques. Later, Rommel and Wagner [4] demonstrated that FPC containing 50–100 mm polycarbonate honeycomb layers functions well with a fluid working temperature between 40 and 80°C. Kessentini et al. [5] presented a FPC with plastic transparent insulation and low-cost overheating protection system destined for heat supply from 80 to 120°C. Hitting higher working temperatures up to 260°C is also possible using glass honeycombs since plastic covers are susceptible to melting at temperatures above 120°C.

Svendsen and Jensen [6] and Svendsen [7] experimentally showed that solar FPC efficiency can be significantly improved by filling the air gap between the absorber and the cover with a monolithic silica aerogel and evacuating to 10 kPa. Duan [8] studied the reduction of front side heat loss by placing the aerogel layer between the transparent cover and the absorber plate showing an increase of 21% in the collector efficiency respecting to the conventional collector. These studies have demonstrated that convective heat losses are significantly reduced by the use of TIM due to the partition of the space between the absorber and the cover-restricting heat transport by convection and thus, a higher performance of FPC was achieved. The test results were encouraging, and a performance comparable to that of evacuated tube collectors was obtained.

Yet, most of the available transparent insulation materials are still not a good choice for high-temperature flat plate collectors. They either cannot withstand high temperature levels because they are made of plastics (mostly honeycomb and capillary materials), they are hygroscopic and cannot withstand the humidity inside the collector (aerogels and so forth), or they are very expensive (glass capillaries).

The use of a moderate vacuum in flat plate collectors is known to reduce top heat losses since the work of Eaton and Blum [9]. The concept of an evacuated flat plate collector was commercially realized and is available on the market. Apart from the higher thermal output, these collectors have the advantage of longer lifetime compared to nonevacuated collectors, because no humidity and condensation problems occur within the casing. Typical interior pressures, which can be maintained economically, lie between 1 and 10 kPa. It means that although convection losses are suppressed, gas heat conduction remains fully developed.

Further, Benz and Beikircher [10] constructed a prototype collector based on the commercially available flat plate collector. To implement high thermal efficiency in the medium temperature range, the thermal losses of the absorber have been reduced using a low emissive selective absorber, a low pressure krypton filling (5 kPa) in the collector casing. The prototype collector has been dynamically tested and has showed very high efficiencies of more than 60% at 100°C. Later, Benvenuti [11] presented a FPC, which is able to reach 300°C. That has become possible by ultrahigh vacuum (1.33x10⁻⁷Pa) maintained by a getter pump powered by the sun. As for the latest studies, Moss and Shire [12] indicate an improvement from 25% for a conventional FPC to 60–65% for vacuum FPC when operating at 140°C above ambient temperatures. More recently, Shire et al. [13] highlight that vacuum FPC collector could provide heat up to 200°C with efficiency greater than 50%.

This paper presents the idea of replacing single glazing, which is used in most of the flat plate solar collectors, with flat vacuum glazing, which, on the one hand, will show a low level of heat losses (low-emissivity coating, high vacuum) and, on the other hand, will demonstrate a high solar energy transmittance. Flat plate solar collectors with low heat loss (at the level of vacuum tube collectors) and with a sufficiently high optical efficiency could be effectively used for integration into building envelopes (residential, industrial), which are widely available.

2. Vacuum Glazing as a Glazing Cover of Solar Collector

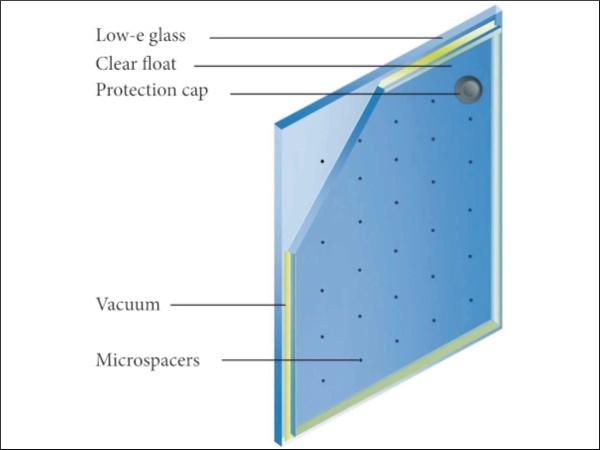
Vacuum glazing consists of two glass sheets sealed together around the periphery. Glass sheets are supported by a pillar array arranged on a regular square grid pattern, and the space between the sheets is evacuated to a pressure lower than 0.1 Pa, thus effectively eliminating both gaseous conduction and convection. Maintaining the pressure below 0.1 Pa for a prospected service life period of 30 years represents a significant engineering challenge. Fang et al. [14] carried out extreme thermal cycling tests.

It was found that the heat conductance at the center region had increased by 10% from which the vacuum pressure within the evacuated space was determined to have increased from the negligible level of less than 0.1 Pa to 0.16 Pa. Later, Koebel et al. [15] investigated the possible sources for pressure increase and concluded that, under consideration for the ideal process conditions, it should be possible to keep the total pressure below 0.1 Pa after 30 years. It is essential to avoid any kind of leaking or microcracking because the quality of the vacuum is directly linked to the thermal insulation performance.

Three different heat transfer mechanisms contribute to the total heat transfer coefficient hg₁-g₂ of the glazing: thermal conduction through a residual gas, thermal conduction through spacers, and radiation heat transfer between the two sheets in vacuum glazing. The total heat transfer coefficient hg₁-g₂ between the glass sheets of a vacuum glazing can be approximated by the simple addition of individual heat transfer coefficients as [16, 17]

where P is internal pressure, σ is the Stefan-Boltzmann constant (5.67x10⁻⁸W/m² x K⁴), Tmean is the average of temperatures T₁ and T₂ of the glass sheets, λ is the thermal conductivity of glass pillars, r is the radius of glass pillars, d is the distance between the pillars, and the effective emittance, εeff, is conventionally written as follows:

Equation (1) is valid for the space with pressure less than 0.1 Pa, that is, high vacuum.

Vacuum glazing already appears in the portfolio of the window suppliers for use in buildings (see Figure 1). Commercially available vacuum glazing with configuration 3-0.2-3 mm has a transmittance of solar radiation of τ=62% and glazing center-of-glazing transmittance U value of 1.1 W/m² x K. The vacuum provides a high level of thermal insulation which reduces heat loss by conduction and convection. However, heat loss can still occur due to radiation. Using low-e coating on the outer surface of the inner glass pane minimizes radiative heat losses.

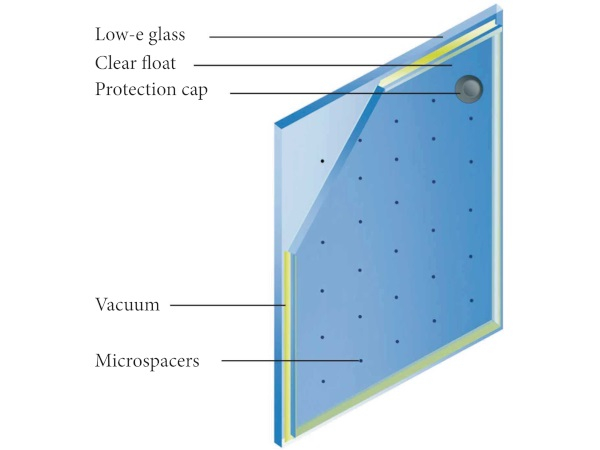
State-of-the-art low-e coatings have been almost exclusively developed for architecture. To uphold the thermal and visual comfort in buildings, coating systems based on silver are primarily used, which can provide for extremely low emissivity (less than 0.03) and high visible transmittance (up to 0.90). Solar transmittance (within the whole solar spectrum range), however, is rarely higher than 0.60. A low solar energy transmittance, caused by the reflectance of low-emissivity coating for the near-infrared radiation (NIR) in the solar spectrum, is unsuitable for use in solar collectors. However, values up to 0.80 and the corresponding higher emissivity (between 0.15 and 0.20) can be achieved by using very thin silver layers, which have been developed in the last years for triple glazing, or with metal oxides (Figure 2) [18]. It is also possible to use the external glass antireflection coatings on both surfaces and thus reduce reflection at the two air-glass boundary surfaces.

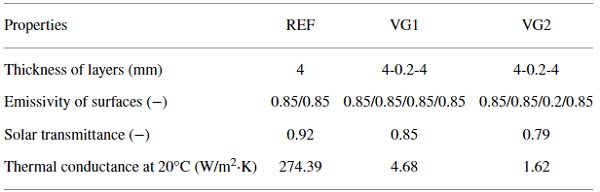
To evaluate the potential of vacuum glazing application in solar thermal collector design, detailed simulations for three different variants of the collector cover glazing have been carried out. Reference variant (REF) is a simple solar low iron glass. The second variant (VG1) has a vacuum glazing based on two low iron glass without any coating. The last variant (VG2) is an advanced vacuum glazing with a low-emissivity coating on the outer surface of the inner glass (position 3). The optical properties of the coating are IR emissivity of 0.2 and solar transmittance of 0.85. Configurations of considered collector glazings are shown graphically in Figure 3. The parameters of the cover glazings used for the comparative study are listed in Table 1.

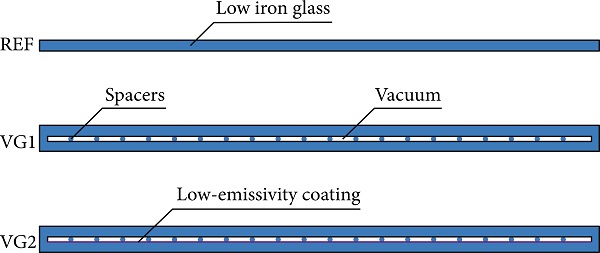
Table 1 Comparison of cover glazing physical properties.

3. Theoretical Model of Solar Flat Plate Collector

3.1. Description of the Model

In order to analyze the thermal performance of FPC with considered variants of the transparent cover, a detailed theoretical model of the flat plate collector has been used. The detailed model originated from design tool KOLEKTOR 2.0 [19] originally developed as the Visual Basic program.

To compare the performance of given glazings, the flat plate collector has been considered to be consisting of an absorber placed in the insulated box covered with a given transparent cover. There is an air gap between the absorber and the cover and between the absorber and its back insulation, both defined by thickness and slope. The absorber is designed as a harp with distribution and riser pipes (defined by length, distance, and diameter). The transparent cover is considered with temperature-dependent thermal conductance according to the equation

where hg₀, hg₁, and hg₂ are coefficients for given cover structures and Tg₁-g₂ (°C) is mean glazing temperature. Thermal insulation layers are considered in a similar way as temperature dependent.

The detailed model of flat plate solar collector allows conducting a detailed calculation of heat transfer in the solar collector. Energy flow from the absorber surface to ambient and from the absorber surface to a heat transfer liquid, together with a temperature distribution in the collector, are calculated in the iteration loops. A solar collector can be specified by a number of detailed parameters, optical properties of glazing and absorber, and thermophysical properties of the main components of a solar collector (frame, absorber, and transparent cover) in the model.

3.2. Basic Equations

The mathematical model for solar flat plate liquid collector solves one-dimensional heat transfer balances. Hottel and Woertz [20], Hottel and Whillier [21], and Bliss [22] developed the simplest assumptions: thermal capacities are neglected and a single value of collector overall heat loss coefficient is considered. Based on these assumptions and considering that the heat transfer is mainly one-dimensional and predominant in the direction normal to the absorber, Duffie and Beckman [23] developed a simplified model (with the electrical analogy) to characterize the solar collector in steady-state conditions. The model solves the energy balance of the solar collector under steady-state conditions according to the principle Hottel-Whillier equation for usable thermal output:

In this equation, Aabs is the absorber area, FR is the collector heat removal factor, τ is the solar transmittance of the collector cover, α is the solar absorptance of the absorber, Gt is the total solar irradiance, U is the overall heat loss coefficient of collector, Tin is the inlet fluid temperature, and Tamb is the ambient temperature.

The main planes of the collector are cover exterior surface (f₂), cover interior surface (f₁), absorber (abs), back insulation interior surface (b₁), back frame exterior surface (b₂), edge insulation interior surface (e₁), and edge frame exterior surface (e₂). A surface temperature is determined for each plane of collector during the calculation procedure. The main collector planes are schematically outlined in Figure 4.

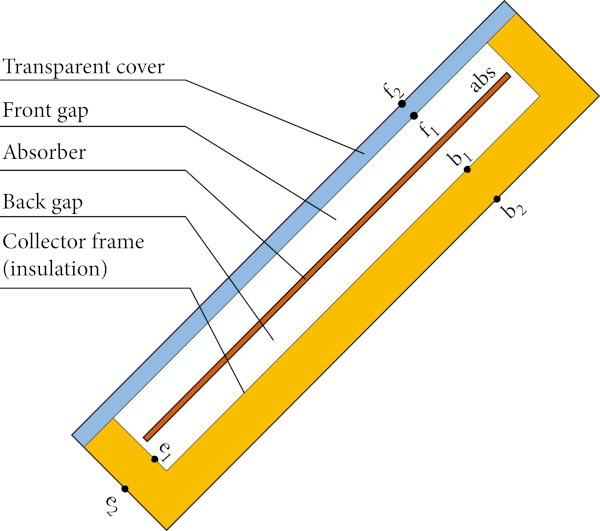
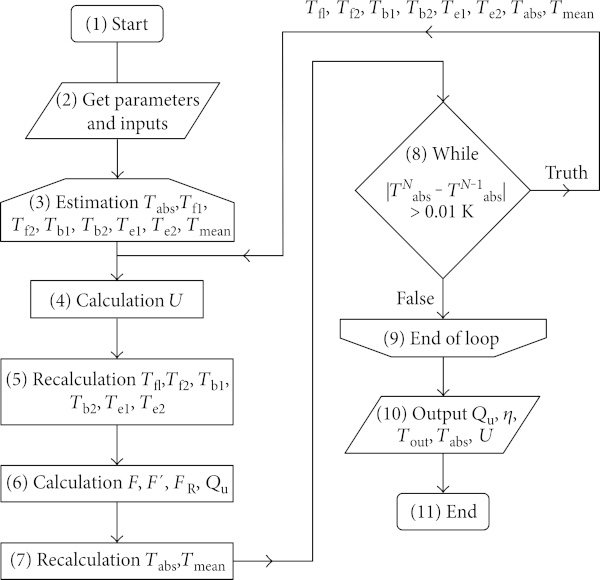
The mathematical model in general consists of two parts: external energy balance of absorber (heat transfer from absorber surface to ambient environment) and internal energy balance of absorber (heat transfer from absorber surface into heat transfer fluid). Both external and internal energy balances are mutually dependent. The overall collector heat loss coefficient U as the main output from external balance is one of the inputs for internal balance. On the other side, mean absorber temperature Tabs as one of the outputs from internal balance is used as a necessary input for external balance. Iteration loop has been introduced to transfer the results from external balance to starting internal balance and the results from internal balance are put to external balance. Loop iterates as long as the difference between absorber temperatures calculated in two adjacent iteration steps is higher than the required minimum (see Figure 5).

3.3. Experimental Validation

The model has been experimentally validated in the frame of solar collectors testing according to the European standard EN ISO 9806 in the accredited Solar Laboratory operated under the University Centre for Energy Efficient Buildings, Czech Technical University in Prague. Solar thermal collectors have been tested to obtain steady-state thermal output at constant operation conditions of inlet temperature (±0.05 K) and mass flow rate (±0.002%) of heat transfer fluid (water) entering collector and at constant climatic conditions of solar irradiation (±1.4%) and ambient temperature (±0.05 K).

Instantaneous efficiency has been calculated from collector thermal output related to total solar irradiation input (incident on collector reference area: gross area). Experimental data points of solar collector efficiency are coupled with uniform uncertainty bars in the graphs. Expanded uncertainty of efficiency and reduced temperature difference have been assessed for experimental data from both type A (statistical) and type B (instrumental) uncertainties considering the coverage factor k = 2 with 95% level of confidence (normal distribution).

The theoretical calculation of efficiency characteristic by the model is subjected to the uncertainty of real collector parameters which are used as inputs for the model. While geometrical parameters are easily available with high degree of confidence, the number of parameters defining the properties of collector parts is found uncertain within narrow range (e.g., absorber and glazing optical parameters, mostly ±2%), middle range (e.g., conductivity of insulation layer dependent on its temperature and density, ±10%), and quite broad range (e.g., emittance of absorber back side and emittance of insulation layer or collector frame, >10%). Therefore, the results of theoretical calculation could be presented as two delimiting curves where the collector efficiency values can be found in reality.

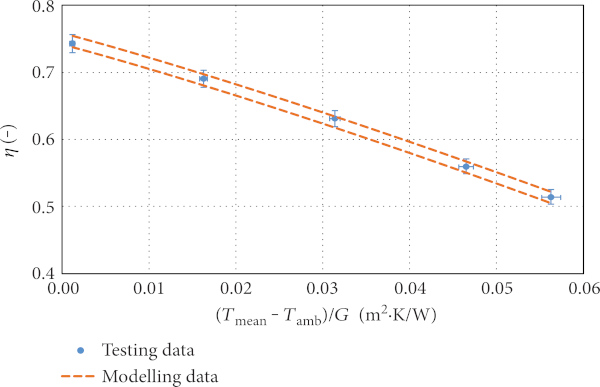
The mathematical model has been validated in the field of atmospheric solar flat plate collectors (top quality solar collectors with state-of-the-art copper laser-welded absorber coated with a high-performance selective coating and solar glazing as a transparent cover). Four different solar collectors have been used for detailed model validation. The majority of solar thermal collector parameters (e.g., thermal conductivity of insulation, the solar transmittance of the glazing, and the emissivity of the absorber) have been measured experimentally to reduce the uncertainty range. The model has also been tested in the case of various values of slope, mass flow rate, wind velocity, and incident radiation. More information about model validation can be found in Shemelin and Matuska [24]. Figure 6 shows experimentally measured efficiency points and theoretically modeled efficiency characteristics. It is evident from the results that simulated efficiency characteristics fit the measurements relatively well, which gives confidence about the developed model.

4. Results and Discussion

Four configurations of FPC were modeled with dimensions 1 × 2 m. All variants have common state-of-the-art copper laser-welded absorber with a high-performance selective coating with absorptivity of 0.95 and emissivity of 0.05. The thickness of the absorber is 0.2 mm and the distance between pipes is 100 mm. Back thermal insulation and edge thermal insulation with thermal conductivity of 0.04 W/m·K have thickness 50 and 20 mm, respectively. The thickness of the air gap between absorber and glazing is 30 mm (except variant VC4, explained below). The difference between considered variants is only in the cover glazing.

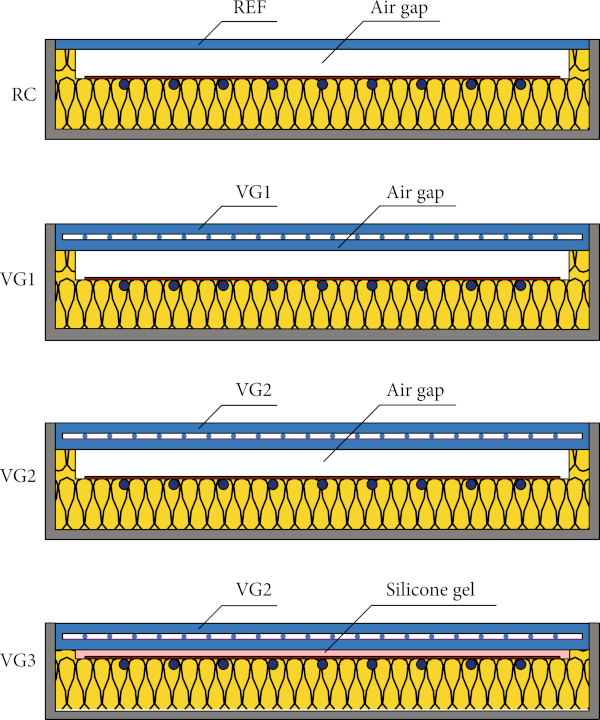
The first configuration of FPC (RC) has a reference glazing (REF) as a transparent cover with the parameters shown in Table 1. The second configuration VC1 has a vacuum glazing VG1 instead of the reference glazing. The third configuration VC2 considers variant VG2 as cover glazing. The last configuration VC3 has a principally different configuration. This variant has no gap between the absorber and the cover. Here, the absorber is bonded to the VG2 by a permanently flexible, highly transparent silicone gel to reduce the thickness of the collector (“slim” collector alternative suitable for building envelope integration). Considered configurations of FPC collectors RC, VC1, VC2, and VC3 are shown in Figure 7.

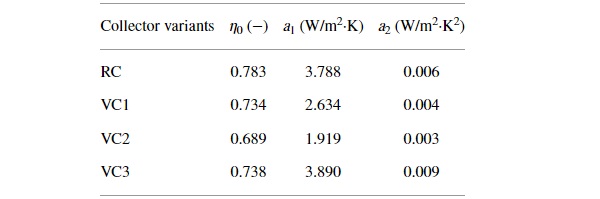
The graph in Figure 8 shows the efficiency curves of considered solar collector variants. With respect to the EN ISO 9806, the collector efficiency η is based on the collector gross area AG. The calculations have been done with the use of early described theoretical detailed model of FPC. The graph shows the difference in energy quality of compared FPC variants. The low slope of the efficiency curve of the VC2 is due to the collector VC2 having two low-e coatings—the first inside the vacuum glazing and the second on the absorber surface. Other variants RC, VC1, and VC3 have only one low-e coating. Solar collector alternative VC3 has lower thermal efficiency than the reference alternative REF. Despite the vacuum layer, higher emittance of the glass low-e coating (0.2) in the VC3 variant instead of absorber coating with emittance 0.05 in the REF variant, brings the total top heat loss to similar value, but optical parameters of the VC3 configuration are lower (lower zero loss efficiency η₀). The resulting coefficients of efficiency characteristics η₀, a₁, and a₂ are listed in Table 2.

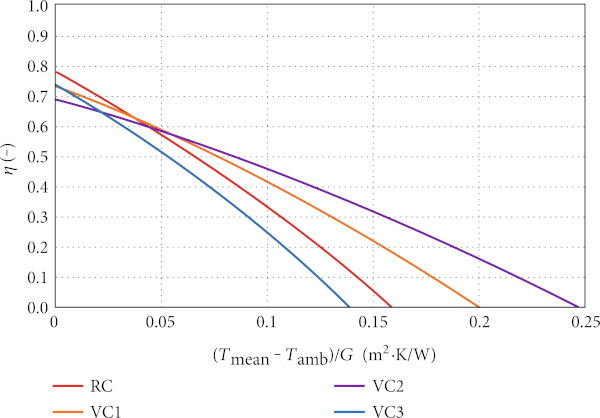
Table 2 Summary of the collector simulation results.

On the other hand, solar collector variant VC3 has the lowest thickness between comparing variants—only 60 mm. Such thickness gives more possibility for integration of FPC into the building envelope because of the slim and compact design. Other variants RC, VC1, and VC2 have thicknesses 87, 91, and 91 mm, respectively.

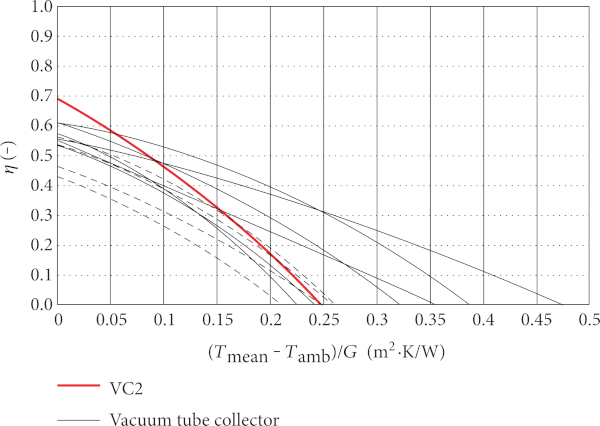
Figure 9 presents the comparison of efficiency characteristics of flat plate collector variant VC2 and vacuum tube collectors (with/without reflector, cylindrical/flat absorber) related to the gross area of a collector. Thermal performance of solar flat plate collector variant VC2 is comparable with that of vacuum tube collectors. Moreover, solar collector variant VC2 shows significantly higher efficiency than the majority of vacuum tube collectors (VT).

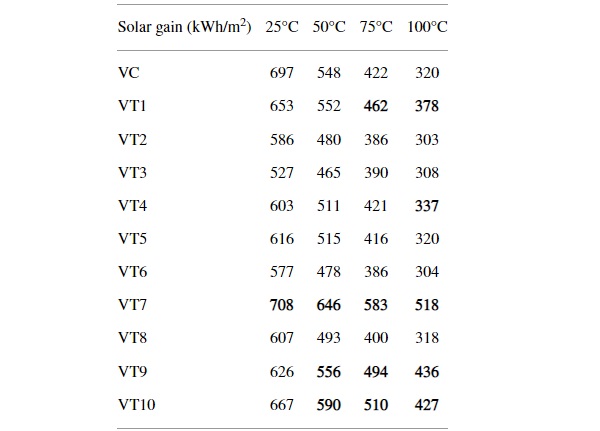
To get a whole picture, the annual performance of the collector VC2 and VT collectors has been modeled using ScenoCalc [25] software for constant operating temperatures 25, 50, 75, and 100°C and climate conditions of Würzburg. The performance and optical characteristics of the compared collectors were used as input data. The results are shown in Table 3. The results of the modeling confirmed that the flat plate solar collector variant VC2 has higher solar energy gains than the majority of vacuum tube collectors up to operating temperature 100°C.

Table 3 Calculated annual solar collector gain with respect to the collector gross area.

5. Conclusions

Different designs of flat plate solar collectors based on a flat vacuum glazing have been theoretically investigated by using the detailed mathematical model to show the potential of vacuum glazing application in solar flat plate collectors. The selected variant VC2 has been compared with state-of-the-art vacuum tube collectors by annual simulation of collector heat output in ScenoCalc. Results have shown that there is a significant potential for increasing the efficiency of solar flat plate collectors by using high-performance vacuum glazing as a transparent cover. Collector variant VC2 shows higher performance than the majority of vacuum tube collectors up to operating temperature 100°C.

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work has been supported by the Ministry of Education, Youth and Sports within the National Sustainability Programme I (NPU I), Project no. LO1605, by the University Centre for Energy Efficient Buildings-Sustainability Phase, and by the project SGS16/212/OHK2/3T/12—Modeling, control, and design of environmental engineering installations.

References