Authors: Benjamin Schaaf & Markus Feldmann
Source: Glass Structures & Engineering volume 9, 147–163 (2024)
DOI: https://doi.org/10.1007/s40940-024-00254-3
Abstract
For glass constructions with a high degree of transparency, facade systems with structural sealant glazing are increasingly being used. However, the use of bonded joints is also suitable for many other applications in glass construction. Even today, the design of bonded joints is still based on the outdated global safety concept according to ETAG 002. Although the safety and predictability of hyperelastic silicone bonds have been continuously shown by research activities during recent years, high levels of safety are still required in the design, which is mainly due to the expected degradation of the adhesive. From a design perspective, it is necessary to consider the time dependency. On the one hand, the bonded joint must be able to withstand variable loads of different strain rates at any time during its service life, taking degradation into account. If the bonded joint is also under a permanent load due to dead load of the glazing, it must also be ensured that the failure time would only be attained at the end of the component's service life. This article presents a fully probabilistic method that considers the degradation of the adhesive as well as various statistical influencing quantities (such as wind effects, manufacturing tolerances or material scattering) and determines a modification coefficient kmod for silicone adhesives under variable loads by calibrating to specified reliability indices. In addition, partial safety factors are determined in accordance with Eurocode 0, which are investigated as part of a sensitivity analysis.
1 Introduction
Adhesive bonding as an alternative to conventional joining methods such as screwing or welding has established itself industrially, particularly since the second half of the last century. The demand from the automotive, aerospace and construction industries for customised adhesives for various applications has increased significantly to date. Adhesive bonding offers many advantages, such as the avoidance of stress peaks for soft adhesives due to surface connection, damping properties or the possibility of equalising tolerances, different thermal expansions of the substrates, avoiding thermal and acoustic bridges, and specifically for glass structures, all glass types can be used.
In structural glass, structural adhesives are used in the form of linear or point-shaped connections. Structural sealant glazing (SSG) is particularly popular in facade construction due to the high transparency of the building envelope. However, as adhesives are polymer materials, time- and temperature-dependent effects and age-related degradation have to be considered when using and designing bonded joints. The current European design concept considers such effects on the basis of a global safety factor, which on the one hand is an outdated design concept and on the other hand includes all strength-reducing influences without weighing these effects. The exact composition of the safety factor is not known.
In order to transfer the design of hyperelastic bonded joints towards the semi-probabilistic design concept according to Eurocode 0, this article determines partial safety factors of the resistance side on the basis of comprehensive experimental data. Furthermore, a full probabilistic approach is presented, that accounts for adhesive degradation alongside several statistical factors (wind impacts, manufacturing tolerances, and material variations). It calculates modification coefficient, kmod, for silicone adhesives through calibration against specified reliability indices.
2 Theoretical background
2.1 Structural sealant glazing
The first facade construction with circumferential silicone bond was erected in 1965 by the company Pittsburgh Plate Glass (PPG) in co-operation with the adhesive manufacturer Dow Corning in the USA (Hot Springs, Ark., Hillard et al. 1977). One of the first SSG systems in Germany was realised in 1985 in the facade of the Institut für Fenstertechnik e.V. (ift Rosenheim, Lieb 2013).
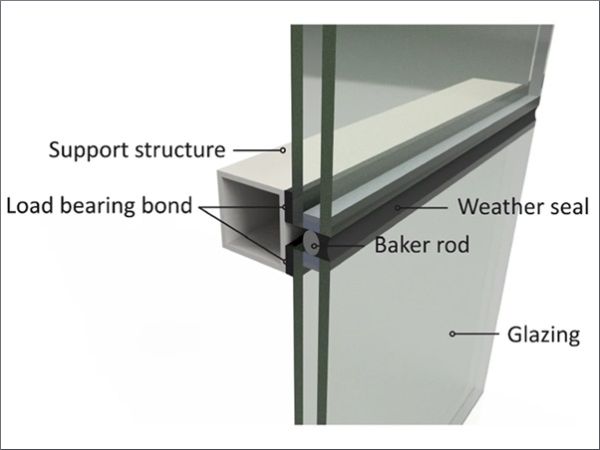
Loads acting on the glazing, such as wind loads, are transferred to the facade substructure, which is usually designed as a mullion-transom system, via the adhesive bond. In addition, the load transfer of the glazing's dead load is also easily achievable via the bonding, but is often not permitted due to official regulations. The adhesive bond is usually manufactured in the factory; however, on-site bonding is unavoidable in certain applications. The structure of a typical SSG system is shown schematically in Fig. 1 (left).

In Germany and Europe, only silicone adhesives with a corresponding approval in accordance with ETAG 002—Guideline for European Technical Approval of Bonded Glass Structures (EOTA 2012) are permitted for use. While silicones have very low strengths and stiffnesses, they are characterised by a high deformation potential. This is essential for compensating for different thermal expansions of the joining partners (stainless steel/aluminium, glass) and is one of the main reasons for using these low-modulus adhesives. In addition, silicones are particularly weather and UV resistant, dampen mechanical effects and reduce stress peaks in the glass due to their continuous load transfer.
To date, the use of SSG has increased significantly, as the desire of building owners and architects for the greatest possible transparency can be met in this way, Fig. 1 (right). The bonded facade systems have also proven themselves in demanding environments with extreme wind loads or earthquake zones (Chiba et al. 2019). Although SSG systems have been used successfully for many years, concerns about load-bearing adhesive bonding are still high in Europe.
2.2 Design of hyperelastic bonded joints
ETAG 002—Guideline for European Technical Approval of Bonded Glass Structures (EOTA 2012) is a guideline document published by the European Organisation for Technical Approvals (EOTA) in 1998, which is used as a basic document for the specification of the essential performance characteristics of a construction product when obtaining a European Technical Assessment (ETA). Along with the technical product requirements for the adhesives to be used, ETAG 002 also contains a concept for the design of adhesive joints in SSG systems. ETAG 002 has meanwhile been converted into an European Assessment Document (EAD) EOTA (2018), which no longer includes the design concept. However, as this is still used by the building authorities, ETAG 002 is referred to below.
The American equivalent of ETAG 002 is the technical standard ASTM C1401—Standard Guide for Structural Sealant Glazing (ASTM C1401), which, like ETAG 002, was published in 1998. ASTM C1401 is the only document comparable to ETAG 002 and is also used outside the American continent. The content of both documents is very similar, but they differ in some respects. However, the design concept using two-dimensional stresses neglecting spatial components and a global safety factor is identical, therefore it is explained in more detail below using ETAG 002.
Within ETAG 002 a two-dimensional stress-based design concept separated for tensile and shear loads is provided. In this concept, the acting forces are related to the cross-sectional area of the bonded joint:

where σ and τ are the normal respective (resp.) shear stresses, F is the force in normal or shear direction and A is the cross section. For a more precise calculation, an additional stress component within the adhesive due to rotation of bonded edges of the surface-loaded glass can be taken into account, which, however, often is neglected.
The design of the bonded joint in accordance with ETAG 002 is based on the (outdated) global safety concept. In contrast to the partial safety concept, in which corresponding partial safety factors are used on the action side and on the resistance side, the global safety concept applies a global safety factor on the resistance side (Spaethe 1992). On the action side, characteristic values are used.
The global safety factor is specified by ETAG 002 as γtot = 6. This value is proposed in the revised version from 2012, but reference is made to nationally determined values. In Germany, the value of γtot = 6 was adopted but can be reduced if additional securities, such as retaining devices in case of adhesive failure or precise calculation of adhesive stresses with Finite Element models, are provided. The composition of the individual influencing variables that lead to the safety factor γtot is not known. It is often also referred to as the “method factor”, as it covers the uncertainties of the design methods and does not represent a safety factor in terms of reliability theory.
ETAG 002 differentiates between short-term and long-term loading (creep) for the shear load to be applied to the bonded joint as part of the design. A permanent tensile load is not intended. The corresponding design values are as follows:

where σdes and τdes are the design values of tensile resp. shear stress under short-term load and Ru,5 is the characteristic fracture stress in tensile resp. shear. According to ASTM C1401 or the Technical Note FKG 01/2012 (FKG 2021) an elliptical criterion can be used to consider for tensile and shear stresses acting simultaneously. ETAG 002 specifies an additional safety factor (creep factor) γc ≥ 10 for the design of a permanent shear load (usually γc = 10). This results for the design:

where τ∞ is the design value of the shear stress under permanent (dead) load. Overall, this results in a global safety factor of 6 for short-term loads and 60 for long-term loads.
The design concept of ETAG 002 is established and easy to use, but also has various weaknesses. Firstly, the design concept is still based on the outdated method with a global safety factor, which was replaced by the semi-probabilistic design with partial safety factors with the publication of the Eurocodes. Furthermore, the adhesive stresses are determined on the basis of a simple manual calculation concept that only distinguishes between a tensile stress component and a shear stress component. However, adhesive joints in SSG systems have a relatively thick adhesive layer, so that a three-dimensional consideration of the adhesive stresses would be necessary here (Schaaf et al. 2020). The high safety factor is also not based on the statistical evaluation of broad experimental investigations, but was determined on a generalised basis (see above). Among other things, this safety factor considers the simplifications of the design, the lack of statistically significant experimental studies on ageing behaviour or manufacturing-related influences and inhomogeneities. The composition and weighting of various influencing factors on the global safety factor are not known.
Studies over the last 20 years have shown that silicones have a very high resistance to ageing and are particularly UV-stable (Dow 2018a). Tests on adhesive samples taken from a 31-year-old SSG facade (1C silicone) in Japan showed almost no changes in material behaviour, even though the façade was exposed to typhoons and two major earthquakes (1995, 2004) during its service life (Chiba et al. 2019). However, the results of accelerated ageing methods according to Schaaf et al. (2023) show that high temperature changes or surfactants can significantly reduce the strength of the SSG adhesives (2C silicones) tested. A more detailed breakdown of the safety level as a function of various ageing influences (under load) would therefore be of considerable interest.
2.3 Time-dependent material behaviour of silicone adhesives
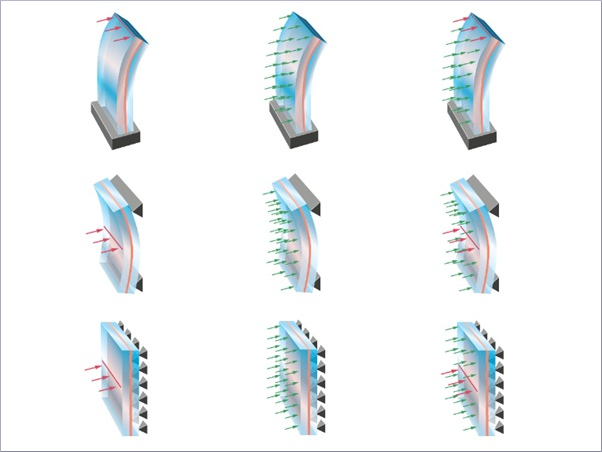
Silicone adhesives show two types of time-dependent behaviour. On the one hand, through viscoelastic material behaviour, which adds a time-dependent component to the material response for each type of load. For example, silicone adhesives show a dependence on the strain rate under quasi-static load or creep or relaxation under constant load, Fig. 2.
The time-dependent behaviour occurs due to molecular movement and rearrangement processes of the polymer network, the speed of which is primarily temperature-dependent. These processes accelerate with increasing temperature. Thermorheologically simple polymers show a time–temperature equivalence. This means that time-dependent processes can be simulated at higher temperatures with significantly less time expenditure. Relaxation and retardation time spectra are thus shifted to shorter times while retaining their shape (Marques et al. 2017).
A further time dependency can be observed with regard to the degradation of the bonded joint. The degradation is caused due to ageing of the polymer. The ageing of polymer materials is understood to be the sum of chemical and physical changes in the material over time, which lead to an irreversible change in the mechanical properties that limit the intended use. The change in the polymer can be attributed to internal and external causes. The internal causes primarily include thermodynamically unstable conditions, such as incomplete polycondensation. The external causes of ageing are environmental influences on the material, such as weather, radiation or chemical exposure. Internal ageing plays a comparatively minor role compared to external ageing. The ageing behaviour of polymers is not fully understood due to its complexity. In particular, the experimental separation of different, overlapping ageing processes represents a major challenge (Ehrenstein & Pongratz 2007). Studies on the ageing behaviour of silicones were conducted by e.g. Van Lacker et al. (2016), Staudt et al. (2018), Drass & Kraus (2020) or Wallau & Recknagel (2020).
According to ETAG 002, a service life of 25 years is assumed for bonded components. The degradation of the adhesive to be expected during the service life is estimated using a comprehensive test program under accelerated physical and chemical exposure. If at least 75% of the unaged reference strength is achieved in subsequent quasi-static tests, the ageing tests are considered to have been passed and the requirement for a service life of at least 25 years is considered to have been met. The ageing resistance of silicone bonds on real components has so far only been documented and published in individual cases, e. g. Lieb (2013).
In order to gain a site-specific insight into the actual material degradation occurring, weathered samples can be used, which are stored on site and tested at regular intervals. With this data, it is then possible to describe the development of damage over time. In Fig. 3 such data from a SSG-facade located in Berlin over a period of 8 years is depicted.
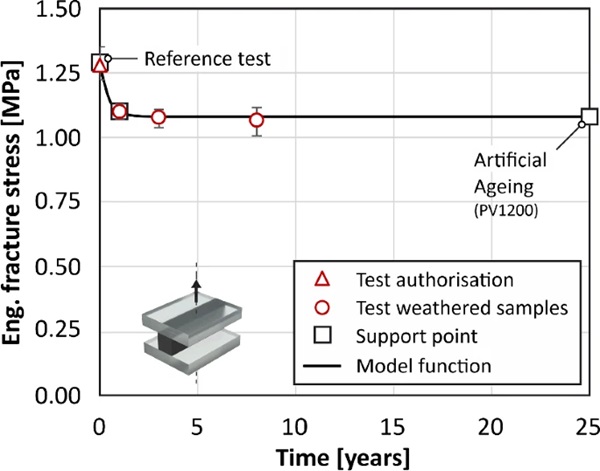
This data was collected using tensile tests using the H-specimen in accordance with ETAG 002. It shows a decrease of the joint’s strength as a function of time. A degressively increasing (declining rate over time) adhesive degradation can be described, for example, using a time-dependent strength function with exponential form (Abeln 2019):
![]()
where A, B and C are model parameter to be determined by experimental data. To determine the required model parameters assumptions regarding the solvability of three independent boundary conditions must be made in advance. The strength f0 at time t = 0 corresponds to the results of unaged reference samples, which are tested immediately after complete curing. Furthermore, the assumption is made that the strength achieved after artificial weathering with test procedure PV1200 (Volkswagen Group) corresponds to the strength after a service life of 25 years. Here, a cycle lasting 720 min is run from −40 °C to + 80 °C with partially controlled and uncontrolled relative humidity with two holding times in each of the temperature extremes. A total of 100 cycles were conducted. With PV1200, the adhesive can be subjected to a high degree of aging beyond the ETAG 002 standard in order to maximise material degradation. A study on ageing shows a significant reduction in strength (ca. 20%) for this artificial ageing regime (Feldmann & Dilger 2022). However, an exact correlation between artificial and real ageing for silicones and polymers in general has not been conclusively clarified. In addition, this assumption implies that almost complete degradation has been reached at this point and that there is no further significant reduction in strength thereafter. The results of the ageing tests after one-year weathering on site are used as a third reference point. This allows the time-dependent degradation to be described as a mathematical function, which will be later used within simulations to determine modification coefficients.
2.4 Target: semi-probabilistic design according to Eurocode for bonded joints.
The overriding objective and wish of many European actors is the regulation of bonded joints of load-bearing silicone adhesive joints within a homogenised European standard. To achieve this, the design on the one hand has to be transferred from the outdated global safety concept (cf. Equations (3) and (4)) to the semi-probabilistic safety concept in accordance with Eurocode 0 (EC 0) (EN 1990). Here, effect and resistance are considered separately and statistical uncertainties are taken into account by two independent partial safety factors. The partial safety factor for the resistance side is discussed in detail in Chap. 3.
In addition, time-dependent effects and the adhesive’s degradation during service life has to be considered within the design concept. This requires ensuring that the design equation is satisfied at all times during the service life with a specified target reliability. A method established in civil engineering for taking such effects into account is the use of a modification coefficient, which at best is to be determined in a full probabilistic method. This coefficient is presented in Chap. 4 and determined fully probabilistically using an exemplary SSG facade.
The partial safety factors and the modification coefficient are also in accordance with the design of glass structures currently been elaborated by CEN/TS 19100 (Feldmann et al. 2023). The publication of prEN 19100-1 (2024) is planned for September 2024. In the coming years, it will be possible to add adhesive bonds to the informative annexes by means of amendments or addendums. According to Sect. 5.4 of prEN 19100-1 elements for load transfer shall fulfil the reliability requirements of EC 0, including durability and resistance against degrading influences. The results for silicone adhesive bonds presented in the following are aimed to contribute to this objective.
3 Determination of partial safety factors
3.1 Introduction and method
In contrast to the global safety concept, which is the basis for the design of SSG bonds according to ETAG 002 and provides for a global safety factor on the resistance side, the semi-probabilistic design concept according to EC 0 contains different partial safety factors for the action and resistance side, which can be determined on the basis of statistical evaluation and calculation methods of the respective variables (Sedlacek et al. 1996). Due to its verification equation E≤R, it represents a practicable, deterministic simplification, which is supplemented by a semi-probabilistic element due to the partial safety factors included, which consider the scattering on the action and resistance side.
The partial safety factor γm covers uncertainties that result from the scatter of the building material properties. It can also be used to consider deviations between the properties determined in laboratory tests and the properties obtained on the structure. The systematic or stochastic errors resulting from simplifying assumptions with regard to the calculation method, cross-sectional deviations, building materials, etc. are taken into account by a separate factor. As such simplifying assumptions are made both on the impact side and on the resistance side, two separate factors result: γRd for the resistance side and γSd for action side. The partial safety factor γM combines the uncertainties of the building material with those resulting from the model uncertainty. The following relationship applies:
![]()
The conversion factor η can be used to consider influences that are not covered by the testing. With regard to adhesives, it would be conceivable to use this factor to cover, for example, degrading effects from the ageing of the adhesive, exposure to cleaning agents or UV radiation in a simplified manner. Based on the ageing requirement according to ETAG 002, this factor could be assumed to be η = 0.75, for example. Within the scope of the method presented in this paper, however, adhesive degradation is considered by a modification coefficient which is determined in a full probabilistic approach. In this way, the degradation can be extracted from the partial safety factor, thus making it possible to consider the modification coefficient depending on load, climatic exposure, creep, etc. in the design equation (cf. Chap. 4).
The partial safety factor γM can be determined depending on the distribution function as follows (Sedlacek et al. 1996, “Material factor approach” acc. to EN 1990):
Normal distribution:

Log-normal distribution:
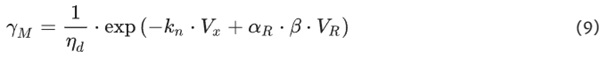
where αR is the weighting factor, β is the reliability index, kn is the fractile factor, Vx, VM, VG, VR are coefficients of variation for test data, model uncertainties, geometry uncertainties and the square root of the sum of the squares of the three aforementioned. The reliability index β is a benchmark for the reliability of the design. The higher it is selected, the less likely it is that the component to be designed will fail during service life. With weighting factor αR the reliability index can be separated into the action and the resistance side. The reliability index will be addressed in more detail in Chap. 4.
A reliability index of β = 3.8 and the weighting factor αR = 0.8 are used for the calculations according to EC 0. The fractile factor can be assumed to be on the safe side with kn = 1.645. Assumptions are made for the coefficient of variation of the model uncertainty VM and geometry VG and the sensitivity to the partial safety factor γM is analysed.
Finally, the determined partial safety factors γM are compared with the current design level according to ETAG 002. As the global safety factor of ETAG 002 does not differentiate between the action and resistance side, but considers both influencing variables in a combined factor, the separation between action and resistance must be resolved for a comparison with the partial safety concept. The comparison factor γvgl is therefore introduced for comparability with the global safety concept, which is calculated as follows:
![]()
The partial safety factor for variable actions is assumed to be γQ = 1.5 in accordance with EC 0. This results in a global safety level equivalent to ETAG 002, in which action and resistance are summarised. The comparison is then to be made against the global safety factor of ETAG 002 γtot = 6.
3.2 Determination of partial safety factors
To determine the partial safety factors γM, the tensile test on the H-specimen with adhesive layer thickness t = 12 mm is used first. In addition to the scattering of the building material in the adhesive bulk, the H-specimen also includes the influence of the transverse contraction restraint of the joining partners (substrates) and thus represents a comparable load situation to the real application. Due to its widespread use for quality assurance and external monitoring, the H-sample is also the most relevant sample type for practical application. The partial safety factors are determined with the use of experimental data from (Feldmann & Dilger 2022). Overall, the results of unaged tensile tests on 136 H-samples of three different approved adhesives are available.
A sensitivity analysis is carried out to study the influence of the variation coefficients of the model and geometry deviations VM and VG on the partial safety factor γM, Fig. 4, since values may differ depending on the calculation method used and production quality. The influence of the assumed distribution function is clearly recognisable. While the lower limit case VM = VG = 0 results in an almost identical partial safety factor of γM =1.1 for normally and log-normally distributed results, the values for the upper limit case of EC 0 VM = VG = 0.2 differ significantly. The partial safety factor assuming log-normally distributed data has a value of γM = 2.2, while that assuming normal distribution has approx. four times the value of γM = 8.2. Overall it can be observed that the partial safety factors are always lower when assuming a log-normal distribution. The values for the safety factors are also very similar to the data determined in Drass & Kraus (2020).
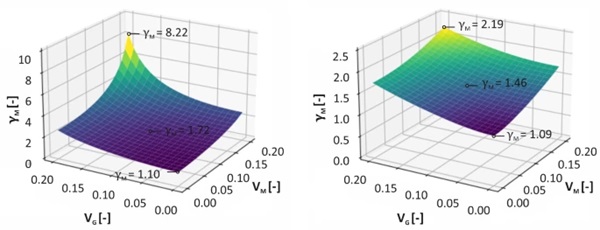
With increasing coefficients of variation VM and VG, there is a non-linear increase in the partial safety factor for both distributions, which can be attributed to the mathematical relationships. However, the applicability of the first order reliability method for a coefficient of variation of V > 0.2 is no longer given according to EC 0. This criterion is met for the coefficient of variation of the test data Vx for all analysed series. The level at which the coefficients of variation VM and VG are to be selected is still to be determined. For example, lower values would be conceivable if a more precise calculation method (FEM, precise material models, etc.) is used or the dimensional accuracy of the joints is ensured by precise manufacturing processes. As the majority of bonded facade elements are factory-made, geometric deviations can be minimised and documented by the quality assurance during production.
The partial safety factors shown in Fig. 4 are weighted means of the three adhesives analysed. The comparison in Table 1 shows that the values determined for the three adhesives are very similar, so that it is expedient to summarise the results. The lowest partial safety factor for the scenarios presented is γM = 1.2, which corresponds to a reduction of the global safety factor according to ETAG 002 by almost 70%. The most conservative value is γM = 2.8, which corresponds to a reduction of approx. 30%.
Table 1 Extract of the partial safety factors determined on the H-samples - Full size table
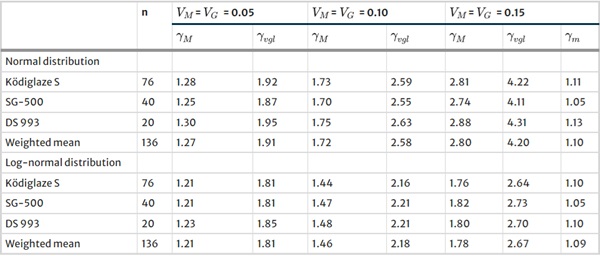
However, the chosen comparison with ETAG 002 is incomplete at this point, as the partial safety factor γM does not consider certain strength-reducing influences, which are covered by the methodological safety factor of ETAG 002 γtot. These include influences caused by adhesive degradation due to ageing, weathering and chemical exposure, production-related inhomogeneities, etc. These influences must therefore be considered in a separate modification coefficient, which further reduces the calculated reduction in the safety level (see Chap. 4).
The tests carried out in (Feldmann & Dilger 2022) on artificially aged samples show a reduction in the expected strength, but no significant increase in the coefficients of variation of the test data. This can also be observed for the influence of the test temperature. The tests carried out in (Drass & Kraus 2020) also show no significant change in the coefficients of variation at high and low temperatures. This means that neither artificial ageing nor the test temperature lead to a change in the determined partial safety factors. It would therefore be possible to determine a partial safety factor γM independently of these two influencing factors.
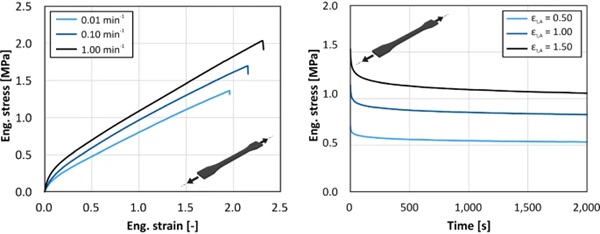
Furthermore, no significant influence of the strain rate on the partial safety factor can be determined. The values shown in Table 2 were determined using the uniaxial tensile test on dog bone samples for three different strain rates, Fig. 5. The independence from the strain rate may be somewhat surprising at first, as the strengths are clearly dependent on this parameter. However, the scatter also increases to such an extent that the coefficients of variation are approximately the same and thus lead to the same partial safety factors.
Table 2 Extract of the partial safety factors determined in the uniaxial tensile test on dog bone samples. Adhesive: Ködiglaze S - Full size table
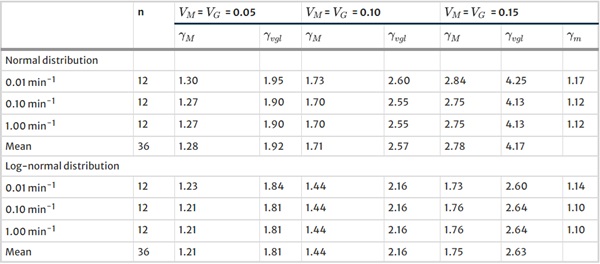
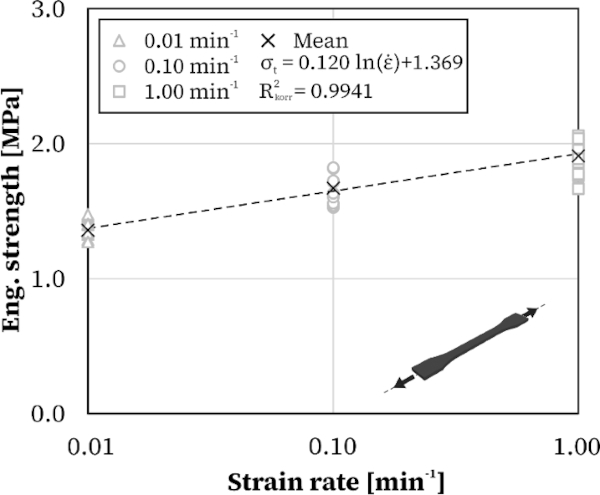
The partial safety factors are very similar and, in some cases, match for different strain rates. Overall, the values differed only slightly from the values determined on the H-specimen. It can therefore be concluded that the partial safety factor determined can be defined independently of the strain rate, ageing and test temperature. As part of future research, it would be conceivable to verify the values determined here using probabilistic exact methods.
4 Determination of modification coefficients
4.1 Introduction
Due to their molecular structure, polymer materials show a pronounced time-dependent material behaviour, which influences the load-deformation behaviour and material failure. Therefore, considering time dependencies within the design concept is essential.
For a simple consideration of the time dependency in the design concept, a modification coefficient (kmod) can be used. The concept of modification coefficients is already established in various fields, such as timber engineering (EN 1995) or structural glass construction (DIN 18008, DIN 16612). The concept of design using modification coefficients is to include strength-reducing effects from time dependency, weathering, etc. on the resistance side in order to reduce the characteristic value of the component resistance Rk:

Due to the simple applicability and the already established use for other materials, the use of the concept of modification coefficients is also suitable for the time-dependent design of bonded joints in glass and facade construction. In addition, the concept is equally transferable to structural bonds, such as those used in steel construction. The procedure for determining kmod is described below and a modification coefficient is determined for an exemplary facade element. The methodology is based on the determination of modification coefficients for timber structures (Köhler 2006; Köhler & Svensson 2002; Köhler & Faber 2003) and modified accordingly for adhesive-specific requirements. Due to the time dependence of the design problem in combination with degrading effects, the determination of the modification coefficient is fully probabilistic.
4.2 Method
For a fully probabilistic calculation two limit state functions have to be considered:
a. Failure due to exceeding the short-term strength.
b. Failure due to exceeding the long-term strength during the service life.
Limit state function a. does not include any dependency on time or service life. It is therefore a stationary consideration of the design problem. Since the non-degraded initial resistance is used, this limit state virtually corresponds to the time t = 0. The probability of failure Pf,S can be determined as follows:
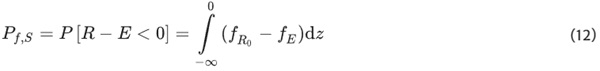
where R, E are resistance resp. effect and fR0, fE are probability density of resistance resp. effect. Limit state function b., on the other hand, considers time-dependent effects, such as the degradation of the adhesive strength. Therefore, this is a transient limit state function, which makes it necessary to consider all points in time within the intended service life. The probability of failure in the interval [0; tL] can be calculated as follows (Enright & Frangopol 1998):
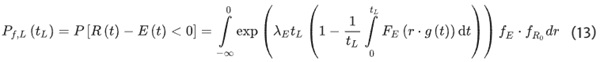
where λE is the frequency of occurrence of the effect, g is the degradation function and FE is the cumulative distribution function of the effect. Both limit state functions can be used to determine the probability of failure over time. The input parameters and their distribution functions are described in detail below. With knowledge of the failure probabilities for the long-term limit state Pf,L, the modification coefficient kmod can be determined. For this purpose, the long-term resistance function
![]()
is calibrated in such a way that a desired target reliability index βT is achieved:
![]()
where Φ⁻¹ is the inverse cumulative distribution function of the standard normal distribution.
4.3 Determination of modification coefficients
Since the analytical solution of Eq. (13) is not known and extremely difficult to determine, the method of Monte Carlo simulations (MCS) is used. Here, the limit states are simulated millions of times with random variables to approximate the probability of failure. The differences between steady-state and transient MCS are explained below.
MCS short-term (stationary) The MCS is performed without time-dependent effects. All input variables refer to the time t = 0. A total of 1,000 runs are simulated. Each run comprises 1,000,000 individual simulations of the limit state function. Thus, a minimum resolution of the failure probability of Pf = 10⁻⁶ is possible.
MCS long-term (transient) The MCS is performed with time-dependent effects. The probability of failure is calculated from 5 to 25 years with a step size of 5, whereby the entire period t∈[1;tL] is always considered with a time resolution of one year. The maximum period of 25 years is based on the intended service life according to ETAG 002. Each run contains 1,000,000 iterations of the limit state function, which also leads to a minimum resolution of the failure probability of Pf = 10⁻⁶. If failure occurs within any time step, the current step is ended and the next simulation step is started. It can be shown that the probability of failure and thus the modification coefficient can already be calculated relatively precisely with the number of runs of the MCS carried out, however, additional simulations increase the statistical significance (Kalos & Whitlock 2008). Due to the time required and the predominantly preparatory nature of these studies, no further simulations were conducted.
Input data For the MCS, an exemplary blocked facade element with the dimensions 2.0 × 3.0 m is selected. The circumferential adhesive joint on all sides has a bite of 10 mm and a thickness of 4 mm. The location of the facade is Aachen and is therefore within wind zone 2 (Germany). As this is a supported bond, only the wind load on the load side is considered. The extreme value distribution according to Gumbel with a reference period of 50 years according to IGF 20604 is used for modelling the wind load. The current draft of EN 1991 recommends the use of a Gumbel distribution. It would also be conceivable to use the Weibull distribution, which is restricted upwards, the Fréchet distribution, which is restricted downwards, or a combined distribution, which is restricted on both sides. The annual probability of occurrence for a strong wind event is modelled using a Poisson process (Last and Penrose 2017). The resulting maximum adhesive stresses are calculated using the extended approach according to ETAG 002. A more precise determination of the stresses would be possible with the help of FEM calculations. However, the integration of a volumetric model into the MCS would mean a substantial additional time expenditure due to the additional calculation time of the FE model. As the stress calculation of the limit state functions is carried out equally for short and long term, it can be assumed that this has no influence on the resulting modification coefficient.
On the resistance side, the strength is used on the basis of the experimental data of the H specimens from Chap. 3. Using statistical test methods (Kol-Mogorov–Smirnov test with Lilliefors correction, Shapiro–Wilk test, Anderson–Darling test), it can be shown that the assumption of a normal distribution for the strength is applicable (Schaaf 2024). Furthermore, production-related deviations in the joint geometry are considered as part of the MCS. Due to the predominantly manual production process, the bite and thickness of the adhesive layer can deviate from the specified dimensions. These deviations are also assumed to be normally distributed. An overview of all input parameters for the stationary simulation of the limit state (short-term) is shown in Table 3.
Table 3 Overview of input parameters (t = 0) - Full size table
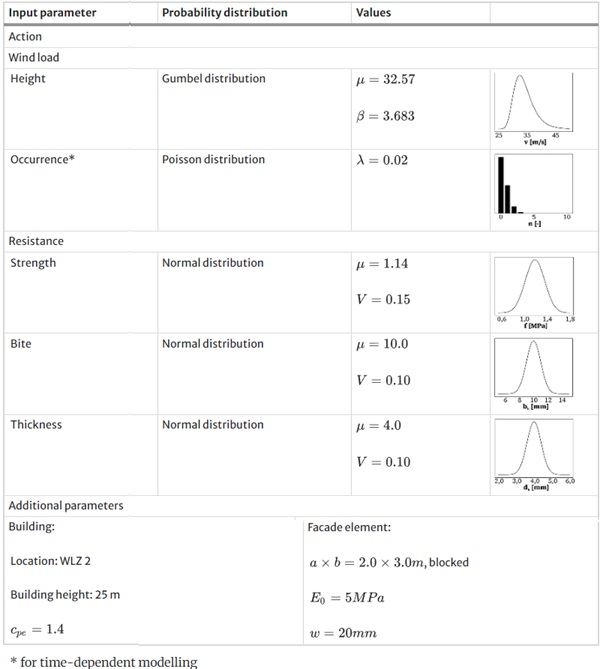
The input parameters shown in Table 3 are also used to calculate the transient limit state function (long-term). However, further time-dependent process parameters have also to be considered within the simulation. The observed time-dependent adhesive degradation is modelled using the damage function described in Eq. (6) (Abeln 2019). The corresponding damage parameters are determined using the experimental data from the ageing tests presented in Fig. 3. Assuming these parameters, an average strength of 84.4% of the initial strength can still be expected after a service life of 25 years. The data collected shows that the majority of degradation occurs within the first three years. With this data, the damage function then predicts only slight degradation until the end of the service life. Further measurements are required to validate this forecast with better significance. However, additional data is not yet available at the time of writing.
In addition to the degradation of the expected strength as a function of the service life t, it is also assumed that the coefficient of variation of the strength increases linearly over time to V = 0.20 (conservative assumption in accordance with EC 0) due to asymmetric aging effects. This results in the following relationship:
![]()
5 Results
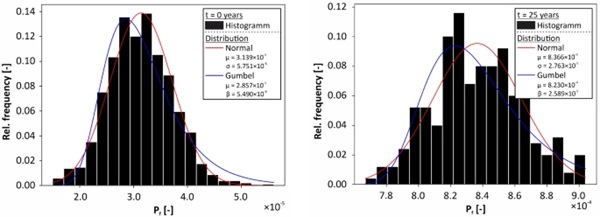
The results of the MCS for the approximation of the probability of failure for the short-term and long-term limit states with an observation period of t = 25 years are shown below as histograms. Distribution functions resulting from the simulation data are also added to the histograms, Fig. 6. The normal distribution and the Gumbel distribution are considered here. The assumption of a normal distribution always provides more conservative failure probabilities than the assumption of a Gumbel distribution. For the limit state at t = 0, the calculated failure probabilities are between = 1.5·10⁻⁶ and 5.6·10⁻⁵. The mean failure probability is 3.14·10⁻⁵. For the limit state after t = 25 years, the mean failure probability, as expected, is higher at 8.37·10⁻⁴. The simulation results lie in a range from 7.67·10⁻⁴ to 9.04·10⁻⁴.
If the mean failure probabilities are shown as a function of the observation points, the failure probability can be interpolated for any point in time using a regressed, exponential auxiliary function (R² = 0.9879), Fig. 7 (left). It is also possible to extrapolate the probability of failure using the analytical relationship. However, since the relationship between time and probability of failure is exponential, extrapolation, e.g. to 50 years, may overestimate the actual probability of failure. With additional MCS, failure probabilities can be determined more precisely, but at a much higher computing cost.
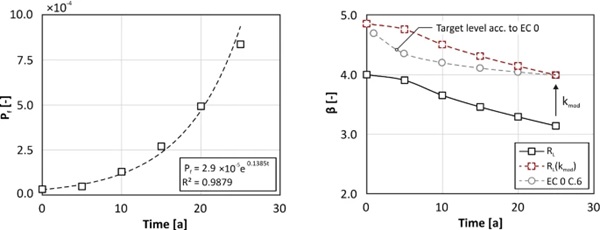
The reliability index β corresponding to the probability of failure is determined according to EC 0 with the probability of failure Pf via the standard normal distribution:
![]()
The target value of the reliability index according to EC 0 for the ultimate limit state (RC 2) for t = 1 year is β = 4.7, for t = 50 years β = 3.8. If fundamental uncertainties are due to statistically independent influences of the action side, intermediate values βn for other reference periods can be determined as follows:
![]()
where β1 is the Reliability index for a reference period of 1 year. However, this relationship cannot be used for degrading resistances. Here, the failure probabilities for the reference periods to be analysed must first be determined separately and then converted into the reliability index. With Eq. (18), however, the time-dependent target values of the reliability index according to EC 0 can now be calculated and compared with the data determined in the MCS, Fig. 7 (right). It can be seen that the reliability level required by EC 0 (circular data points) is not achieved over the service life (black square data points). Due to the degrading effects, the reliability index also decreases more rapidly over the service life.
With the help of the determined failure probabilities, the modification coefficient kmod for hyperelastic silicone adhesive bonds can be calibrated. Further MCS are required for this. According to EC 0, βT = 3.99 is used as the target reliability index for 25 years. In addition, further target values are considered in order to study the influence on the resulting kmod. With help of the modification coefficient, the reliability level can be raised to a specified target value (red curve in Fig. 6 (right)). Figure 8 also shows the influence of different strengths on kmod as a function of the probability of failure.
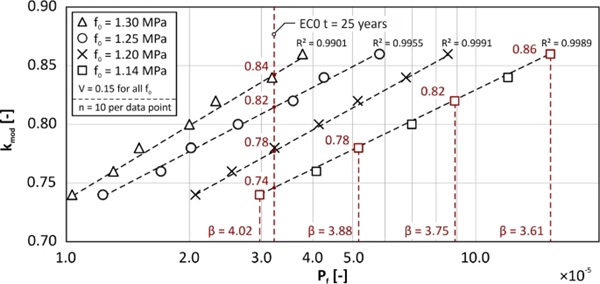
The following influences on kmod can be observed:
- With increasing strength, kmod increases As the probability of failure is reduced with increased strength, a lower reduction via kmod is required within the design in order to achieve the required reliability level.
- With increasing target reliability, kmod decreases When the required reliability level is increased, i.e. the tolerated failure probability is reduced, the long-term resistance within the design must be reduced accordingly by a reduced kmod.
- A kmod > 1.0 means that the reliability determined in the simulation is above the required target reliability; if kmod < 1.0, the target reliability is not achieved and a reduction of the resistance is required for the design according to Eq. (11).
The simulations show that a realistic value for a modification coefficient kmod for the design of silicone adhesive joints with a target service life of 25 years, considering variable loads for the reliability required according to EC 0, lays between approx. 0.75–0.85 considering different parameter variations. A conservative assumption would therefore be a modification coefficient of kmod = 0.75. However, the strength used here is very conservative, as outliers have been included in the data set, which reduce the expected value of the strength and increase the coefficient of variation accordingly. Average strengths of 1.2 to 1.3 MPa are more realistic, which leads to coefficients of 0.78–0.85. Against this background, a modification coefficient of kmod = 0.8 is proposed. This value is comparable to the modification coefficient of weathered timber structures (0.70/0.80) (DIN 2020). However, the simulations presented in this chapter and the determined coefficients should be seen as examples. To derive a reliable modification coefficient, additional simulations are required, considering other locations and component geometries. Furthermore, permanent loads should also be included in the calculation by determining a separate coefficient for unblocked bonded joints. The time-dependent limit state function is to be extended in such a way that, in addition to failure due to variable actions, creep failure during the service life due to permanent loads is also taken into account. For this purpose, experimental studies on time dependence or time-dependent failure, which have not been finished at time of publication, must be included as part of future research.
6 Conclusion and outlook
Adhesive joints of SSG systems are currently designed according to the outdated global safety concept with a global safety factor on the resistance side. This paper discusses two necessary topics in order to transfer the design of such adhesive joints to the semi-probabilistic concept according to Eurocode 0. Based on extensive experimental data partial safety factors are calculated according to the first order reliability method and compared with the current safety level according to ETAG 002. It can be shown that these values are very similar for three approved adhesives studied. Additionally, they are also independent of the strain rate. Compared to the safety factor according to ETAG 002—considering the different safety concepts—the partial safety factors are considerably reduced. However, in contrast to the safety factor according to ETAG 002, the partial safety factors do not include any time-dependent effects such as the ageing of the adhesive.
Consequently, Monte Carlo simulations are used to approximate the fully probabilistic solution of the time-dependent design problem, whereby various influencing variables on the reliability index and the resulting modification coefficient are analysed. Within the scope of the investigation, modification coefficients between 0.75 and 0.85 are calculated. A realistic assumption for kmod for silicone adhesive joints in structural glass construction could be approx. 0.80. However, the determined values are only exemplarily as more simulations with different parameters, e.g. geometry, location, etc., have to be considered. Furthermore, permanent loads have to be included in a next step to assure that creep failure does not occur within the target service life of unblocked bonded joints. In addition, further data to determine the actual ageing of silicone adhesives would be of great interest. In addition, the stress-based two-dimensional design concept should be extended for more complex adhesive joint geometries. A three-dimensional strain-based design is discussed in (Schaaf 2024), for example. On further consideration, the semi-probabilistic design concept with respect to time dependency can also be applied across systems to structural stiffer bonded joints, e.g. in steel construction (Feldmann et al. 2006, 2017). However, individual safety factors and modification coefficients must be determined. For this purpose the application-specific requirements and loads for these adhesive systems (e.g. epoxy resins, polyurethanes, etc.) must be taken into account.
References
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Institute of Steel Construction - RWTH Aachen University, Aachen, Germany | Benjamin Schaaf & Markus Feldmann
Corresponding author
Correspondence to Benjamin Schaaf.
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.