This paper was first presented at GPD 2023.
Link to the full GPD 2023 conference book: https://www.gpd.fi/GPD2023_proceedings_book/
Authors:
- Laura Galuppi (1),
- Massimo Maffeis (2),
- Ali Haydar (1,2),
- Gianni Royer-Carfagni (1,2)
(1) Department of Engineering and Architecture, University of Parma, Parma (PR), Italy
(2) Maffeis Engineering SpA, Solagna (VI), Italy
Abstract
The uneven heating of architectural glazing, typically resulting from shielding by the frame and by irregular shading, produces an uneven temperature distribution, which may induce thermal stresses leading to breakage, a condition often referred to as “thermal shock”. Here, a simplified engineering approach for the calculation of the temperature field in the panel is presented, which accounts for the presence of shadows and frame, as well as for the different heat exchange phenomena. The model is validated by comparisons with the results of a numerical method based on Biot’s variational approach, with reference to various case studies, accounting for the daily changes in the solar radiation and environmental temperature.
Introduction
One of the most frequent causes of breakage in architectural glazing is the thermal stress deriving from non-uniform temperature fields in the glass pane, induced by the shielding of the contouring frame, as well as by shadows on the panel cast by sunshades, fins, parts of building, etc. Indeed, since glass has relatively poor properties in terms of heat conduction, it is prone to heat up and cool down in an uneven manner within the single panel, therefore causing a differential thermal expansion. This results into a simultaneous mechanical action of warm parts trying to expand and cold parts trying to withstand this expansion, leading to compressive stress in the warm part and tensile stress in the colder one. The precise assessment of the temperature field is hence of paramount importance for safety and durability of building skins.
The temperature distribution is governed by different heat exchange phenomena: heat convection and heat radiation exchange with external/internal environment, solar radiance, heat conduction among parts of the panel at different temperatures, and heat storage. Consequently, it depends on a large number of environmental and geometric parameters, such as seasonal and daily variation of internal/external temperatures and solar radiation, material thermal properties, pane inclination and orientation. In the design practice, reference is made to simplified approaches from Standards [1]. Dedicated commercial Software can provide sophisticated analyses but, realistically, it can be used only for important projects.
Here, a dedicated 3D semi-analytical formulation [2], [3], based on the variational principle proposed by M. Biot in the 1950s [4] and specifically conceived for non-uniformly irradiated architectural glazing, is presented. Results are compared with those obtained via a simplified engineering approach [5], [6], based on the assumptions that temperature is approximately uniform in different pane regions, and that conductive heat exchange between adjacent regions occurs in interface strips. The basic equations governing the simplified model are revised, and paradigmatic examples are presented for the sake of comparison, considering the time variation of external temperature and sun radiation.
Biot’s variational method
A semi-analytical Finite Element formulation, based on Biot’s variational principle [4] for heat transfer, has been recently presented in [2]. Its major advantage is that the field variable is not the temperature but the heat displacement vector field, related to the temperature by the equations of heat conduction and energy conservation.
This formulation implemented in a numerical approach, called in short BVM-FEM, is specific for the study of glass panes, considered monolithic in the present version of the code, with projected shadows and/ or contour frames shielding the sunlight, under variable conditions in terms of internal/ external temperature and solar radiation. In the numerical implementation, distinction is made between the heat fluxes in the in-plane directions (governed by the heat transfer with the surrounding environment), and in the thickness direction (dictated by heat conduction between differently irradiated regions) by using ad hoc shape functions. This particular implementation, allowing to use only one element in the plate thickness, has been validated in [3]. Once the 3D temperature distribution is evaluated, traditional FE software can be used to determine the thermal stress.
The simplified engineering approach
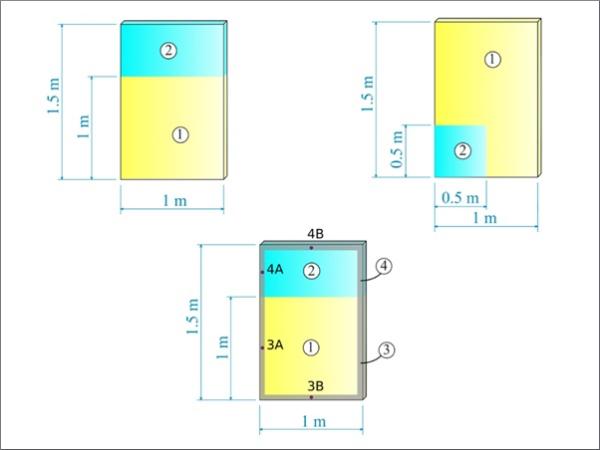
A simplified engineered approach has been proposed in [5] to estimate the temperature fields in a monolithic glass panel, as a function of daily and seasonal changes in the solar radiation and environmental temperature. The model has been further extended to the study of the temperature distribution in insulating glass units [6]. One of the major hypotheses is that the glass plate is thermally thin, a condition usually verified for architectural glass, so that the temperature can be assumed to be uniform in the thickness. The proposed method takes into account the possible presence of a frame that contours the panel, as well as of shadows cast by external screens, by dividing the panel in regions considered thermally homogenous, classified according to their location and shading according to the following scheme:
- Region 1: glass directly invested by the solar radiation;
- Region 2: shaded glass;
- Region 3: glass trapped in the window frame, in contact with region 1;
- Region 4: glass trapped in the window frame, in contact with region 2.
For the i-th region, of area Ai,i =1..4, the timedependent temperature Ti (t) is evaluated by establishing a transient energy balance, accounting for the heat flows due to different heat exchange phenomena, i.e.,
• Heat convection exchange with the external and internal environments, at temperatures Text (t) and Tint (t), respectively:
![]()
where hext and hint are the external and internal heat transfer coefficients.
• Heat radiation exchange with the external and internal environment:
![]()
where ε is the glass emissivity, σ is the Stefan-Boltzmann constant, and Tsky (t) is the effective sky temperature (temperatures are here expressed in K).
• Absorption of the solar energy, denoted to as G(t), striking the panel:
![]()
where α is the glass absorptivity, and φi is a coefficient accounting for the presence of shadows, set equal to 1 in region 1, 0.1 in the shaded region 2, and to 0 in the framed regions 3 and 4 [1].
• Heat conduction among adjacent regions i and j; by assuming that the heat conduction length is βs, being s the panel thickness, the heat flow is

where λ is the glass thermal conductivity, and Lij is the length of the interface between i-th and j-th regions. According to the results presented in [3], β =10 is assumed in the sequel.
• Heat storage per unit time in the volume Vi = sAi of the i-th region

where ρ is the mass per unit volume, and cp the glass specific heat.
Notice that, in agreement with [1], it is assumed that the convective/radiant heat transfer with the surrounding environment affects the temperature distribution also in the regions covered by the frame. Reference values for the coefficients appearing in eq.s (1-5), as well for the environmental parameters, are usually prescribed by Codes [1]. For each considered region, the energy balance can be written by requiring that the energy storage is the sum of the heat flowing into the considered region, i.e.,
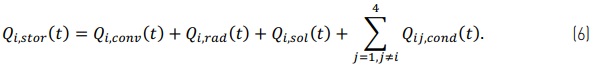
This is a system of four coupled first-order differential equations, which governs the time-dependent temperatures Ti (t),i = 1..4. The system can be easily solved with standard numerical techniques.
Examples and comparisons
The considered model problem is that of a rectangular monolithic glass pane 1 m × 1.5 m × 12 mm, where uneven radiation conditions on the glass surface are produced by external shadowing elements, as well as by the bite of the contouring frame. The three different considered geometries are shown in Figure 1. The temperature distribution is evaluated, by considering a winter scenario, during a whole day. Following [5], external temperatures Text (t)=Tsky (t) are approximated with a sinusoidal law and vary between -20 °C and 0 °C. The solar energy absorption G(t) is assumed to be null during the night hours (between 7:30 p.m. and 4:30 a.m.), while in the light hours it is approximated with a parabolic trend, with a maximum of 880 W/m². Results obtained with the Simplified Engineering Approach (hereafter compactly denoted as SEA), by solving eq.s (6), will be compared with those obtained with the full 3D analyses performed by using the BVM-FEM, providing a non-uniform distribution of the temperature on the glass thickness.
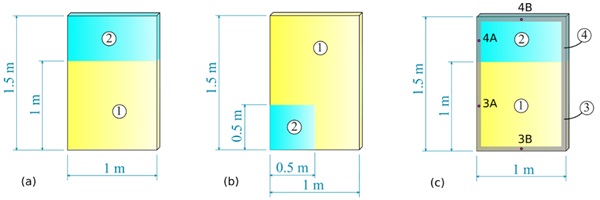
Example 1
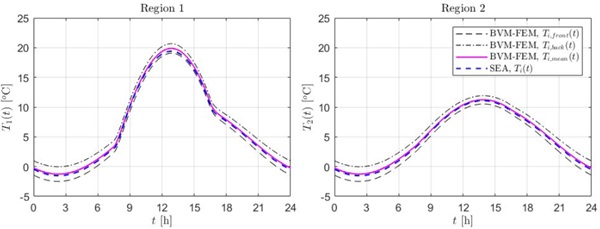
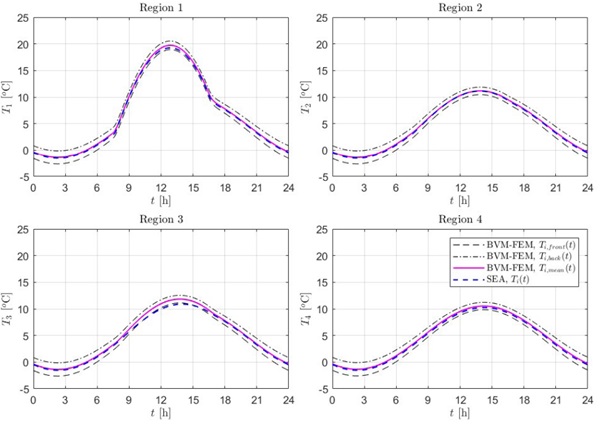
Consider the rectangular glass panel of Figure 1a, where the upper region 2 is shaded, while the complementary region 1 is directly hit by the solar radiation. Figure 2 shows the daily evolution of the temperature in these regions, obtained with the SEA and the BVM-FEM. In the second approach, temperatures are evaluated at points of the regions 1 and 2 where they are substantially uniform (i.e., at a sufficient distance from the interface), and both the temperatures at the external panel surface, Ti,front (t), and at the rear one, Ti,back (t), are plotted together with their average Ti,mean (t). Notice that the time-evolution of T1 (t) is strongly influenced by both the parabolic variation of G(t) and the sinusoidal trend of Text (t), while T2 (t) is mainly affected by Text (t), since region 2 is only partially irradiated.
The SEA, despite is simplicity, allows to correctly capture the time-variation of the mean temperature along the day. Indeed, the maximum error is less than 0.5 °C in region 1, and of about 0.3 °C in region 2.
Example 2
To investigate the influence of the shadow shape, consider now the glass panel of Figure 1b, presenting a square shaded region. Notice that the SEA does not allow to capture the precise influence of the shadow shape, but it can account for this important condition in an indirect way, being the temperature distribution influenced by the area of the different regions and their contact length, appearing in eq. (4). Figure 3 shows the comparison between the results obtained with the SEA, compared with the outcomes of the BVM-FEM, again in terms of front, back and mean temperature on the two regions. Also in this case, the accuracy of the SEA is excellent, being the maximum error of about 0.4 °C on region 1, and less than 0.2 °C on region 2.
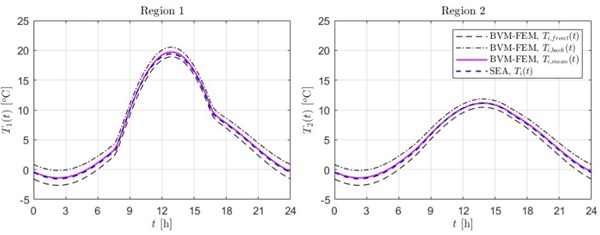
Example 3
Consider now the pane of Figure 1c, whose upper 30% portion is shaded, contoured by a frame of width 50 mm. In this case, since the framed regions (3 and 4) are very narrow, their temperature field is affected by the closeness of the interface (the temperature cannot be evaluated “at a sufficient distance from the interface”). Here, the temperature values obtained with the BVM-FEM at the middle of the strip, in particular at points 3A and 3B (for region 3) and 4A and 4B (for region 4), have been considered, and it has been verified [3] that T3A (t)=T3B (t) and T4A (t) = T4B (t). These results are compared with those obtained with the SEA, with reference to the different regions, in Figure 4.
From the graphs, it is evident that the temperatures in the framed regions, T3 (t) and T4 (t), are influenced by the solar radiation only indirectly, due to the heat-conduction from the adjacent irradiated regions. Due to the in-plane heat conduction, the framed region 3, in contact with region 1, is hotter than region 4. Again, there is a good agreement between the BVM-FEM and the SEA. The greatest error, of about 1 °C, is recorded on Region 3; on Regions 1, 2 and 4 it is consistently lower (maximum error of the order of 0.5 °C, 0.2 °C and 0.3 °C, respectively).
Conclusions
Here, a simple engineering analytical model to evaluate the temperature distribution in unevenly heated architectural glazing, has been demonstrated in paradigmatic examples by comparisons with a more sophisticated numerical code. The engineering model is based on the definition of thermally homogeneous regions, for which the temperature, evaluated by means of the energy balance, is assumed to be uniform. Despite its simplicity, the proposed model allows to correctly capture the time-variation of the mean temperature in the different regions along the day. Indeed, when compared with the numerical 3D implementation of the thermal problem, undoubtedly more accurate, the obtained mean maximum error is of the order of 0.5 °C. The engineering approach can provide an accurate estimation of the thermal stresses, inasmuch they are mainly influenced by the in-plane temperature gradients, rather than by the (small) temperature variation along the glass thickness.
Acknowledgements
This research has been supported by Maffeis Engineering SpA, Solagna (Vi), Italy.
Bibliography
(1) NF DTU 39 P3 (2006) Travaux de vitreriemiroiterie – Partie 3: Mémento calculs des contraintes thermiques. Standard, CSTB.
(2) Galuppi, L., Royer-Carfagni, G. (2023). Thermal analysis of architectural glazing in uneven conditions based on Biot’s variational principle: part I - description of the finite element modelling. Glass Struct Eng, 8, 41–56.
(3) Galuppi, L., Royer-Carfagni, G. (2023). Thermal analysis of architectural glazing in uneven conditions based on Biot’s variational principle: Part II - validation and case-studies. Glass Struct Eng, 8, 57-80.
(4) Biot, M. A. (1970). Variational principles in heat transfer. Oxford University Press, London.
(5) Galuppi, L., Maffeis, M., Royer-Carfagni, G. (2021). Enhanced engineered calculation of the temperature distribution in architectural glazing exposed to solar radiation. Glass Struct Eng, 6(4), 425-448.
(6) Galuppi, L., Maffeis, M., Royer-Carfagni, G. (2022). Engineered calculation of the uneven in-plane temperatures in Insulating Glass Units for structural design. Glass Struct Eng, 7(1), 71-99.