Calibrated Numerical Approach for the Dynamic Analysis of Glass Curtain Walls under Spheroconical Bag Impact

Authors: Alessia Bez, Chiara Bedon, Giampiero Manara, Claudio Amadio and Guido Lori

Source: Buildings 2021, 11(4), 154, MDPI

DOI: https://doi.org/10.3390/buildings11040154

(This article belongs to the Collection Innovation in Structural Analysis and Dynamics for Constructions)

Abstract

The structural design of glass curtain walls and facades is a challenging issue, considering that building envelopes can be subjected extreme design loads. Among others, the soft body impact (SBI) test protocol represents a key design step to protect the occupants. While in Europe the standardized protocol based on the pneumatic twin-tire (TT) impactor can be nowadays supported by Finite Element (FE) numerical simulations, cost-time consuming experimental procedures with the spheroconical bag (SB) impactor are still required for facade producers and manufacturers by several technical committees, for the impact assessment of novel systems. At the same time, validated numerical calibrations for SB are still missing in support of designers and manufacturers. In this paper, an enhanced numerical approach is proposed for curtain walls under SB, based on a coupled methodology inclusive of a computationally efficient two Degree of Freedom (2-DOF) and a more geometrically accurate Finite Element (FE) model.

As shown, the SB impactor is characterized by stiffness and dissipation properties that hardly match with ideal rigid elastic assumptions, nor with the TT features. Based on a reliable set of experimental investigations and records, the proposed methodology acts on the time history of the imposed load, which is implicitly calibrated to account for the SB impactor features, once the facade features (flexibility and damping parameters) are known. The resulting calibration of the 2-DOF modelling parameters for the derivation of time histories of impact force is achieved with the support of experimental measurements and FE model of the examined facade. The potential and accuracy of the method is emphasized by the collected experimental and numerical comparisons. Successively, the same numerical approach is used to derive a series of iso-damage curves that could support practical design calculations.

1. Introduction

Glass curtain walls notoriously represent a challenging issue for designers. Given that they must satisfy specific performance requirements in terms of energy, light, acoustic insulation, etc., curtain walls represent in fact a physical barrier for the occupants. As such, careful consideration is required for their structural assessment, even under extreme events. In this regard, several literature studies have been dedicated to the analysis of glass facades under various loading conditions, including blast events, seismic actions, etc. [1,2,3,4,5]. Among others, the assessment of facade capacities under soft body impact (SBI) still represents one of the most frequent accidental design actions (i.e., due to impact of occupants) and also one of the most severe performance limitations, especially against the potential risk of fall [6], see Figure 1.

So far, several research efforts have been spent on the analysis of the impact performance of glass systems. Relevant outcomes are available in the literature, but they are mostly related to specific design applications like simple glass panels [7], glass balustrades [8,9], load-bearing glass columns [10], existing traditional windows [11] or novel laminated glass windows [12]. In [13], a systemic experimental and numerical analysis has been dedicated to the analysis of glass constructional elements under the pendulum test, with a focus on the numerical description of the impactor features. This study follows the extended investigations reported in [14,15,16], in which the dynamic performance of glass panels under tire impact has been explored with the support of experimental and numerical tools. Often, within the research community, the SBI performance of glass elements is primarily explored for automotive applications [17], or in terms of danger for people [18,19], while a generalized methodology still lacks for the mechanical characterization of curtain walls.

In this paper, a careful consideration is paid for curtain walls under a spheroconical bag (SB) impactor, with the support of full-scale experiments, Finite Element (FE) numerical models (Code Aster [20]), two Degree of Freedom (2-DOF) modelling techniques and practical design tools that could be useful in support of daily practice (i.e., iso-damage curves). In more detail, Section 2 summarizes the key features of experimental methods in use for curtain walls under SBI, as well as the basic theoretical background of impact. Differing from “ideal” conditions, as shown, the SBI response of curtain walls is affected by the features of the facade (impacted body), by the type of impactor (SB or TT) and by the impact features (impact point, drop height, facade features and impactor properties). A novel approach is thus presented in Section 3, based on the coupled analysis of a simplified 2-DOF model and a more geometrically accurate FE model of the curtain wall unit object of study. The procedural steps that are used for the optimal calibration and minimization of the analysis efforts are hence discussed. 

Section 4, in more detail, presents an experimental campaign carried out on curtain wall unit specimens under a multitude of impact configurations (15 repetitions and arrangements), while the reliability of the proposed procedure is shown in Section 5. Given that the calibrated 2-DOF parameters are derived from a multitude of impact configurations, the general validity of the procedure is shown. Some further design outcomes are presented in Section 6, where comparative analyses are proposed for the optimal definition of the input impulse. For comparative analysis of the proposed methodology, additional numerical results are also derived from the commercial software SJ MEPLA [21] (“MEPLA”, in the following). In conclusion, iso-damage curves are presented in support of design for glass curtain walls under SBI.

2. State-of-Art and Background

2.1. Standardized Experimental Approach

Glass curtain walls and facades are recognized to have a crucial role in buildings, given that they are expected to offer a physical barrier against falling of the occupants, and a physical protection from potential outdoor events. Accordingly, safety must be especially ensured against accidental impact events. The fall of possible debris, in the event of glass breakage, must be prevented with the protection of pedestrians that could be nearby the glass facade. Defenestration events must be also prevented. In this context, the use of laminated safety glass represents an efficient design solution. However, many other performance indicators must be properly assessed, at the component and assembly level.

For a long time, the SBI performance has been assessed through experiments, based on standardized testing procedures. Usually, these tests are carried out in-situ, or in laboratory conditions on full-scale mock-ups. The mostly used impactors, see Figure 2, are the spheroconical bag (SB) and the twin tire (TT). The former is filled with glass spheres and has a total weight M = 50 kg, while the latter consists of two pneumatic tires inflated with 3.5 bar air pressure. A steel mass (M = 50 kg) is included within the tires themselves. In this research paper, the tires consisted of Vredestein V47 pneumatics [22].

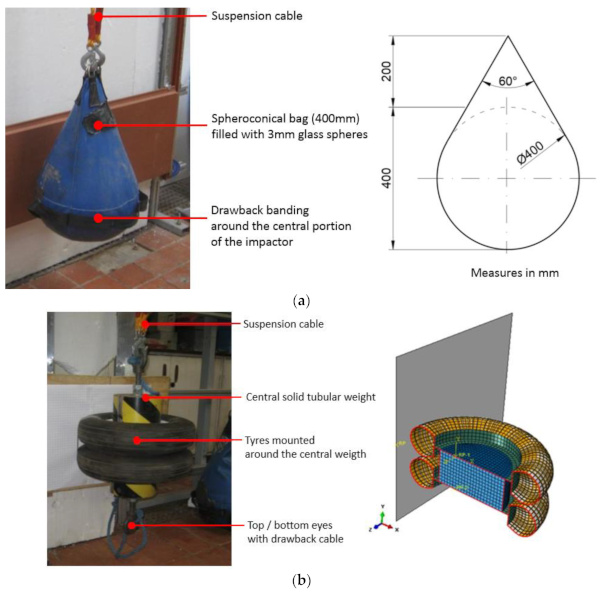
Major issues for manufacturers of glass curtain walls under SBI, in this regard, currently derive from the existence of a number of National norms and regulations that follow different procedures.

So far, the International EN 12600 standard [23] introduced the TT pendulum protocol at the European level, with the aim of replacing the SB impactor. The TT is in fact more easily describable in its basic components. Further, the German DIN 18008-4 (Annex A) regulations [24] confirmed the possibility of TT impact FE numerical simulations in place of full-scale experiments. In the years, several research studies highlighted the realistic description of TT features and effects with numerical tools [9,13,14,15,16,25]. The MEPLA commercial software, in this regard, also developed a lumped spring-mass model able to capture (with limits) the TT features, and thus offer a geometrically and mechanically simplified numerical model in support of design (see Section 2.2 and [26,27,28]).

On the other side, a set of standards exists that prescribe a pendulum setup still based on the SB impactor, and includes the French Cahier CSTB 3228 [29] and NF P 8-301 [30] for vertical or horizontal glazing, the CWCT TN 76 [31] (vertical glazing) and ACR[M]001:2005 [32] (horizontal elements) standards in the United Kingdom, but also the American ANSI Z97.1 document [33]. The performance evaluation after impact requires one to assess whether the glass system is able to pass a given setup, and to classify the specimen capacity depending on the lack of breakage, or on the size and features of cracks and fragments (if any). However, given that the cited references represent the primary regulation for various National technical committees, this condition forces facade designers and manufacturers to follow the original SB approach. In this regard, the use of efficient numerical tools could simplify the SB impact assessment for various practical applications.

Besides, calibrated parameters for SB simulations are not available in the literature, and cannot be replaced by TT formulations. The Newman’s hypotheses discussed in [34] asserts the greater severity of impact tests carried out with the TT impactor, rather than the SB. The latter is in fact recognized to have a behavior that is hardly comparable to an elastic body under impact. Moreover, the SB impactor generally offers a greater dissipative capacity, compared to the TT. Most of the dissipative phenomena are related to the glass spheres inside the bag of Figure 2, which are not bound to reciprocal movements. Accordingly, ideal theoretical assumptions for impact estimates are generally over-conservative for real experimental setup configurations with the SB, thus requiring more advanced characterization and calculation procedures.

In this paper, the proposed methodology aims at exploring the difference of SB and TT parameters, towards the definition and calibration of practical recommendations and practical approaches to equalize the SB effects to the TT, for a given envelope unit under SBI.

2.2. Numerical Analysis of Glass Curtain Walls under Soft Body Impact

2.2.1. Ideal Impact

For a curtain wall under the impact of a pendulum in accordance with Figure 2, the dynamic features and response of the system can be notoriously sensitive to a multitude of parameters. As such, the reliable description of the input time history for the impact force can be challenging. The actual phenomenon still derives from the “ideal” impact configuration, but it should be further characterized. According to the classical theory, the limit condition is represented by an elastic impactor against a rigid body, and the expected force time history is expressed as:

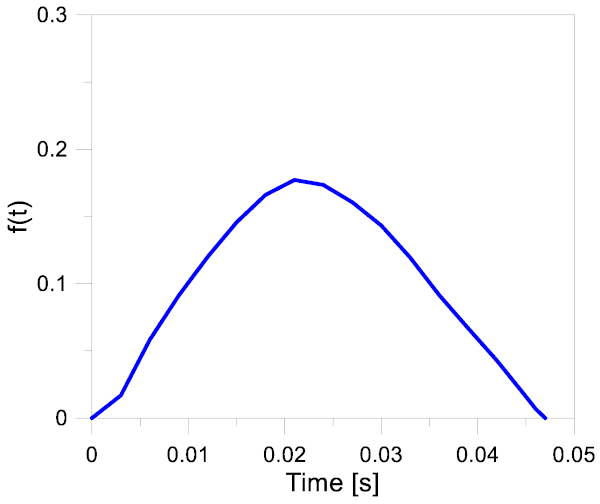
where the key input parameters are represented by the impacted surface A; the peak pressure p, that depends on the drop height of the impactor; and the time factor f(t), whose typical trend is proposed in Figure 3.

For a rigid impacted surface and elastic impactor, the incoming impulse Iid on a given surface A can be rationally calculated as:

with MP denoting the mass of the impactor and vP its velocity, at the time of impact. Assuming that MP and vP are the assigned input data, the corresponding impact energy can be hence predicted in:

and thus:

The above assumptions, although theoretically accurate, involve a severely conservative description of input features, both on the side of the impactor and on the side of the impacted glass panel. Equations (2)–(4), more in detail, represent an upper limit (or “ideal”) condition, since the real behavior is generally affected by the intrinsic flexibility of the impacted glass panel (i.e., stiffness of facade components, compared to a rigid surface), as well as on the impactor features (i.e., type, size, stiffness, impact energy), which manifest in a series of dissipative phenomena.

2.2.2. Simplified Design Approach

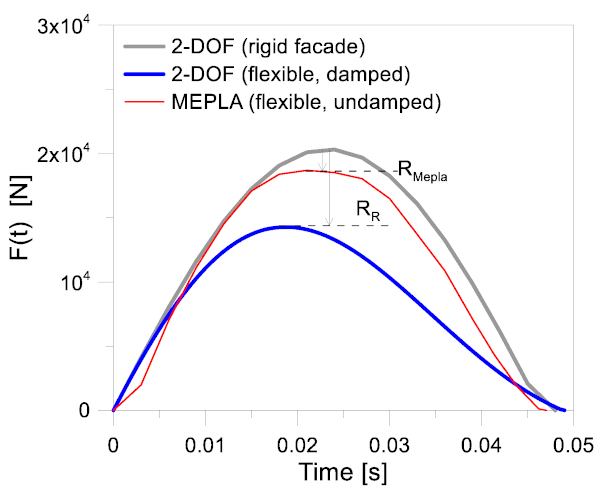
The MEPLA computer software is largely used for structural glass design applications, given that it is specifically tailored to the needs of the civil engineering industry and offers some a useful support for the efficient analysis of standard configurations. For impact purposes, the software proposes a lumped spring-mass model that calculates a time history of impact forces for the so-called “default pendulum impactor” loading case based on EN12600 [23]. This “default pendulum impactor” option, compared to more refined modelling techniques (as for example in [9,13,28]), represents a simplified tool for the description of a test setup with TT impactor. At the same time, the approach assumes the hypothesis of elastic impact on a flexible, undamped facade unit. The final result, compared to an ideal impulse as in Section 2.2.1, is a partially reduced impulse IMepla:

in which the reduction factor RMepla < 1 accounts for some intrinsic aspects of the real dynamic phenomenon and bodies involved in the impact event. Research studies in [26,27] and others extensively verified the accuracy of such a schematic representation of the TT impactor, giving evidence of a good correlation with experimental records of various glazing systems. On the other side, see for example [13,28], the lumped mass-spring model cannot equal a geometrically refined characterization of TT impactor, in terms of component features and pressurized air volume in the tires. As a matter of fact, moreover, it lacks of an accurate geometrical and mechanical characterization of the impactor, as it would be required for the SB. Further effects, in the cited procedure, finally derive from the lack of dissipation features, both for the glazing system and for the impactor. These limitations end in a potential over-prediction of the expected accelerations, displacements and strains for the curtain wall, and thus in a consequent over-design of the load-bearing components against SBI.

3. Design Approach for Glass Facades under Soft Body Impact

3.1. Concept, Assumptions and Goals

In the current investigation, a new calibration procedure in support of design is proposed and validated by means of full-scale experimental tests. Further, the MEPLA software is used for comparative analyses on curtain wall units under variable SB impact. The goal is to predict the impact response of a given glass facade, by taking into account the actual impact force, with the support of analytical and numerical estimates in place of cost- and time-consuming experimental protocols. The flexibility and damping contributions are taken into account both on the side of the curtain wall and the impactor, thus allowing to obtain a generalized solution of the design issue. In this way, the amount of experiments can be reduced to a minimum, or even cancelled. From a practical point of view, see Figure 4, the magnitude of the impulse is expected to be:

with

where RR is a refined reduction coefficient able to account for the boundary conditions and dynamic properties of the curtain wall under SBI. The advantage of Equation (7) is that the maximum theoretical impulse can be minimized to reliable estimates, while keeping mostly constant the total duration of the “ideal” impact event. To achieve this goal, however, some key procedural steps must be taken into account (Section 3.2).

3.2. Proposed Procedural Steps

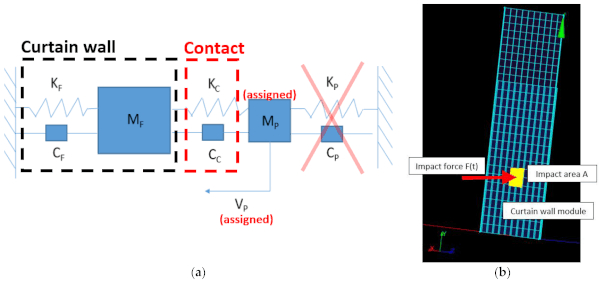
For a given glass curtain wall under SBI, a coupled approach based on a simplified 2-DOF model and a more accurate numerical model (Code Aster) is considered for the modular unit in Figure 5. For the 2-DOF model in Figure 5a, more in detail, components with subscript “F” refer to the facade systems, while the subscripts “P” and “C” are used for the impactor and the contact parameters. The design procedure herein proposed is achieved (and generalized) through the sequence of steps that are schematized in Figure 6. In the STEP 0, the features of the curtain wall and the desired impact energy Eimp are defined for the loading condition of interest. Given that MP = 50 kg, the corresponding impact velocity vP and the related ideal impulse Iid are first derived from Equations (3) and (4). At this stage, both the 2-DOF and the FE models of Figure 5 must be properly characterized.

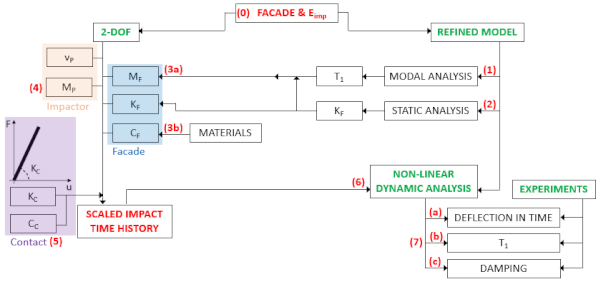
Considering the FE model in Figure 5b, the curtain wall module must be described with careful attention for materials, components, boundaries (Section 5). Then, a frequency analysis is carried out to predict the fundamental vibration period of the undamped system (T1, STEP 1). The equivalent stiffness KF of the curtain wall represents another key input parameter, given that it is affected by the facade features and also by the point of impact (STEP 2). Such a parameter can be derived from the same FE model, under a unit force that is statically assigned to the desired impact point, and thus based on the corresponding static displacement. The knowledge of T1 and KF is the starting point for the 2-DOF characterization, given that the equivalent mass MF for the modular unit can be calculated as (STEP 3a):

Finally, on the side of the curtain wall, the damping term CF must be also specified (STEP 3b), based on:

where ξ is a total damping term (including the effects of materials, possible damage propagation, and aero-elastic effects). A detailed calculation approach would require the experimental calculation of test records (i.e., logarithmic decrement, see Section 5). Given that the proposed approach is intended for efficient early-stage design calculations, however, the accurate total damping ξ may not be available. As a reference, accordingly, a minimum value should be set at least in:

thus accounting for the material properties in use. Based on literature data, for example, the input values in Equation (10) can be expected in the order of 1% for glass, 2% for the soft layers and the metal frame, respectively [35,36,37,38].

Depending on the type of impactor in use (see Figure 6) the input parameters must be then properly specified to account for the TT or SB effects (STEP 4), as well as the effect that they transfer to the facade (STEP 5). Given that MP and vP are known, in accordance with the 2-DOF model in Figure 5a, such parameters are described in the form of a simple mechanical law for the contact itself (i.e., KP and CP are set to 0). The contact parameters KC and CC that are required for STEP 5, in other words, are responsible of the actual force (and time history features) that the impactor can transfer to the curtain wall, depending on the time of contact and on the impactor features. In this research study, all these parameters were iteratively calibrated, based on experimental results and numerical fitting (Section 6.2). Once the above parameters are known, the result of the 2-DOF model is a scaled impact force that implicitly accounts for the reduced impulse IR in Equation (6), and can be thus assigned to the FE model, to perform non-linear dynamic analyses of the system (STEP 6).

In presence of full-scale impact experiments (STEP 7), the FE dynamic analysis can be assessed towards the test records, or give a realistic prediction of the experimental outcomes, in terms of deflection in time (a), period of vibration of the facade (b), damping of the system (c), but also stress peaks, reaction forces, etc. In the present study, STEP 7 is specifically used for the validation. Otherwise, for curtain walls under SBI, the herein proposed calibrated parameters can be used for general applications.

Major efforts are in fact spent for an accurate characterization of the impactor and contact parameters for the 2-DOF model (STEPS 5 and 6), and the reliability of this characterization is supported by the extended experimental program inclusive of various impact configurations (Section 4 and Section 5). The developed FE models, in particular, are able to capture the features of the impacted system and also the impactor/contact parameters, and this is proved by the close numerical match of the experimental displacement peaks for all the examined configurations. As far as a similar description of facade components and features is taken into account for a given curtain wall module under variable SBI configurations, the proposed method results in a FE model that can be still used for SB setup investigations. In this way, based on the input facade/impact energy assumptions (STEP 0), the correction coefficient RR in Equation (6) is implicitly accounted in the 2-DOF procedure and the calculated impact force. For both the SB and TT impactors, simplified mechanical laws are thus presented in Section 6, while the final outcomes of such a calibration procedure are presented in Section 6.1 and Section 6.2, giving evidence of the accuracy and potential of the overall procedure.

4. Experimental Analysis of Curtain Walls under Soft Body Impact

The numerical approach herein proposed was validated towards experimental measurements collected from SBI tests carried out on identical configurations of curtain wall panels under various impact conditions. The experiments were carried out in Vittorio Veneto (Italy), during February 2020, with an average ambient temperature of 8–10 °C.

4.1. Materials and Methods

The impact experiments were specifically focused on the dynamic analysis of a single curtain wall specimen configuration as in Figure 7a, with 15 test repetitions. The reference panel was characterized by the presence of:

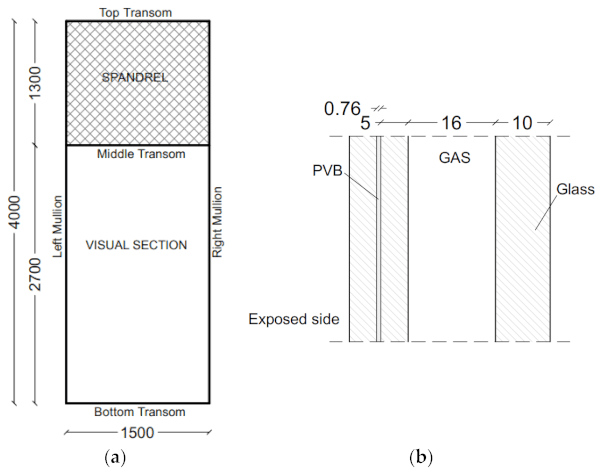
• a sandwich spandrel section, with a total size of 1500 × 1300 mm2, that was positioned on the top of the specimen (for insulation purposes only). The cross-section included an aluminum foil (3 mm in thickness) and a steel foil (2 mm the thickness, S355 the resistance class [39]), while a mineral wool panel was used to fill the gap.
• a visual section (Figure 7b), with a total size of 1500 × 2700 mm2, composed of an insulated glass unit (16 mm the cavity thickness) with a 10 mm thick, monolithic layer (on the unexposed side) and a laminated safety panel (two 5 mm thick, annealed panels and a bonding 0.76 mm thick PVB film) on the exposed side. All the glass layers consisted of annealed glass [40].

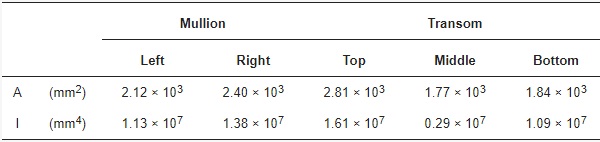
The specimen included a supporting aluminum frame (alloy type 6063-T6 [41]), with sectional properties reported in Table 1. The mechanical connection between the visual glass panel and the supporting frame was ensured by structural sealant joint (DowsilTM 993 silicone [42], with a joint thickness of 10 mm). The so-assembled prototype was thus clamped with four steel brackets to the test bench frame (two at the top and two at the bottom corners of the frame), see Figure 8a.

Table 1. Nominal properties of the frame. Key: A= cross-sectional area, I= second moment of area.

To measure the out-of-plane deformations of the specimen under impact, three laser sensors were used. All the laser sensors were installed on the unexposed side of glass, in some key control points of the curtain wall unit that have been detected as:

• LS1: center of the glass panel;
• LS2: mid-span section of the right-side mullion; and
• LS3: mid-span section of the bottom transom.

To ensure the exhaustiveness and reliability of experimental measurements, the SBI tests were performed on glass specimens under different:

• type of impactor (TT or SB impactor);
• impact point (P#n, with a fixed impact energy and impactor); and
• impact energy (Eimp, with a fixed impact point and impactor).

To this aim, as also in accordance with Figure 9, five different impact points were selected on the curtain wall specimen, namely represented by:

• P#1: impactor at the glass center, 1 m above the bottom transom;
• P#2: impactor at the glass center;
• P#3: impactor on the middle axis of glass, 0.5 m above the bottom transom;
• P#4: impactor at a distance of 0.35 m from the right mullion, 1 m above the bottom transom;
• P#5: impactor at a distance of 0.35 m from the right mullion, 0.5 m above the bottom transom.

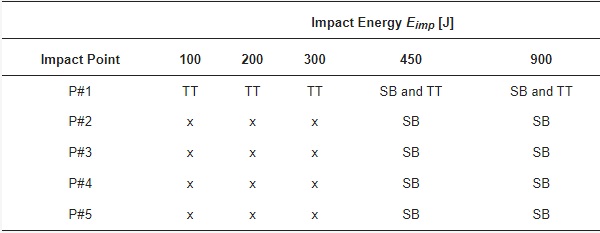
The experiments were first carried out for the specimen with spheroconical bag impactor. Successively, the more severe TT impactor was used for additional test repetitions. The final combination of testing configurations is summarized in Table 2.

Table 2. Selected experimental configurations. Key: TT = twin tire impactor; SB = spheroconical bag; x = not available.

4.2. Test Results

The analysis of test results was focused on the measured out-of-plane deformations of selected control points, as well as on the visual detection of possible cracks in glass, so as to evaluate the performance class of the tested specimens, according to the standards requirements. For all the loading configurations in Table 2, it is important to highlight that no glass damage was observed experimentally. In terms of FE numerical investigation herein discussed, accordingly, the lack of failure and crack propagation in the glass panel facilitated a simplified characterization of materials, especially glass, that was assumed to behave linear elastically (Section 5).

5. Finite Element Numerical Analysis

5.1. Solving Approach

The numerical study was carried out with the support of the Code Aster open-source computer software, is integrated into the Salome Meca platform [43]. A series of dynamic non-linear analyses was carried out under various impact configurations. The software choice was intentionally guided, at the time of the research study, by the need of a freely accessible FE software that could be accessible to designers, but at the same time highly refined to support non-linear dynamic simulations.

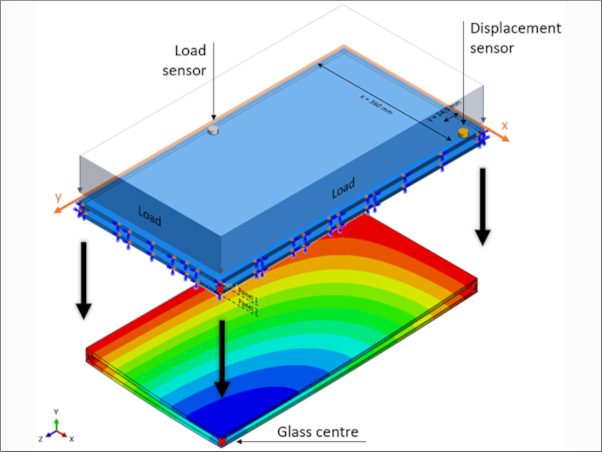
At the initial stage of the study, to make sure that the reference Code Aster FE model was properly calibrated in its key input parameters, a very high number of benchmarks has been developed under static and dynamic conditions. Based on sensitivity studies, the final FE assembly shown in Figure 4 resulted in brick elements (with 20 nodes and quadratic shape functions) for the glass panel and the sandwich spandrel. In the case of the supporting frame members, mono-dimensional beam elements were used. The mesh size was set in 10 mm. Besides such a series of basic assumptions, the attention was focused on the detailing of several influencing parameters that are summarized in the following sections.

5.2. Reference FE Model for SBI Simulations

The reference FE numerical model was realized to reproduce the actual geometry and dynamic behavior of the tested curtain wall specimens earlier described in Figure 7. Besides the reference mesh pattern that was chosen in Section 5.1, special attention was required for the calibration of some other important parameters.

5.2.1. Geometry

The top spandrel, being composed of a sandwich section with insulation purposes only, was first simplified and numerically represented in the form of an equivalent monolithic section. The material properties were characterized in the form of elasticity and density able to reproduce the actual bending performance of the nominal spandrel section. An equivalent thickness concept was taken into account for the laminated glass section, given that PVB foils under short term and impact events are typically associated to a relatively stiff Young’s modulus. Accordingly, a monolithic glass section of 10 mm in thickness was taken into account in place of the 5 + 5/0.76 composite panel.

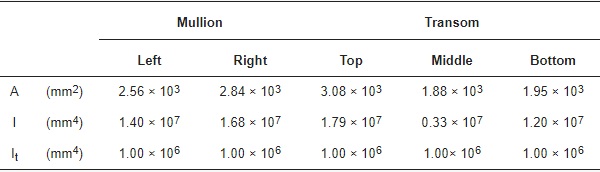
Regarding the aluminum frame members, the attention was spent for the description of the inertial effects due to the presence of non-metallic thermal barrier components. Compared to inertial values reported in Table 1, the thermal barrier contribution was generally observed to greatly affect the overall period of vibration of the examined curtain wall system. Accordingly, the effective inertial properties for the frame members was herein calculated as prescribed in the Annex C of the EN 14024:2004 document [44]. The final input data are summarized in Table 3.

Table 3. Nominal properties of the frame members. Key: A = cross-sectional area, I = second moment of area; It = torsional moment.

5.2.2. Gas Cavity

As known, the gas cavity represents a key parameter for insulated glass units, given that it is notoriously responsible of “load sharing” phenomena for the involved glass panels [45,46,47]. To simulate this interaction for the glass units, various numerical approaches can be found in the literature, and most of them are based on fluid interactions in the cavity, so as to include ideal gas formulations:

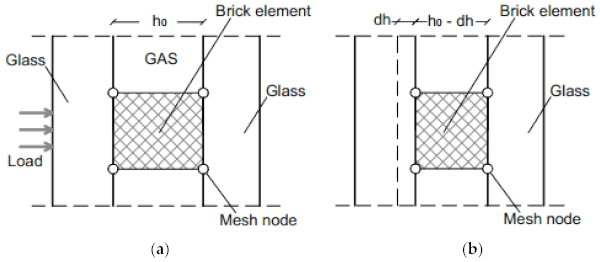
In the current paper, given that the Code Aster software does not include any fluid interaction for the dynamic non-linear domain, a major simplification was assumed for the gas infill, see Figure 10.

In more detail, an equivalent, linear elastic material was taken into account, with an input modulus of elasticity that was calibrated under the assumption of an isothermal transformation for ideal gases (i.e., a transformation that can often occur under impact test conditions). For a single brick element of the gas cavity, the governing law:

was thus taken into account.

According to Equation (12), the volume of a single brick element can be expressed as the product of its un-deformed surface area Agas (that was ideally kept constant under deformations) and the un-deformed thickness h0 (with h0 = 16 mm the cavity thickness, in this study):

As far as small thickness variations dh are considered for the cavity subjected to external compressive loads agreeing with Figure 10, the pressure-deformation trend can be derived from measurements of the corresponding brick mesh nodes. Under the simplified hypothesis of a linear elastic material in the small-deformation regime, the so-derived constitutive law allows then to extrapolate an equivalent elastic modulus for the gas infill, that is:

with Δp the pressure variation calculated from Equation (11).

In the present study, the equivalent modulus was estimated in Eeq,gas = 0.08 MPa. Besides the intrinsic limits of such an assumption, compared to more accurate calculation approaches, the equivalent modulus Eeq,gas can be considered a reliable value, as far as the expected cavity deformations due to impact are small (i.e., in the same order of magnitude of h0 itself). On the other hand, Eeq,gas should be separately estimated under different geometrical configurations (and especially for variations in the un-deformed thickness h0).

5.2.3. Materials

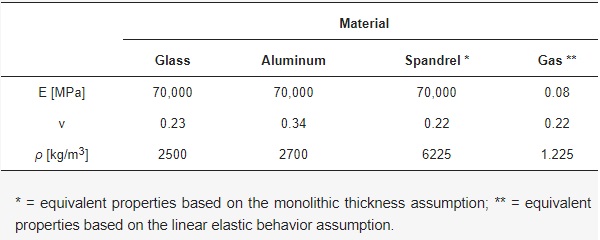
Given that no visible damage was detected in the reference full-scale experiments (see Section 4.2), linear elastic constitutive laws were used for all the materials in use. The corresponding Young’s modulus E, Poisson’ ratio ν and density ρ are summarized in Table 4. It is worth noting in Table 4 that no failure stress was explicitly considered for annealed glass (ft = 45 MPa the characteristic nominal value under quasi-static tensile loading [40]).

Table 4. Input mechanical properties for the materials in use.

The post-processing analysis of FE data was thus focused on the evolution of maximum deflections for the tested specimens, but also on a necessary analysis of stress peaks in the module components. Major attention was spent for glass, so as to ensure the reliability of a linear elastic material characterization for FE purposes. Among other constructional materials and literature studies, the discussion in [2] and Figure 11 about annealed glass confirms the well-known sensitivity of its compressive and tensile strength to strain rate. This effect typically results in the so called Dynamic Increase Factor (DIF) that can be quantified—for impact and impulsive configurations—in up to 3–4 times the nominal strength value ft under quasi-static loads. Simple stress estimates can be thus carried out towards the DIF value of strength [3,48,49].

5.2.4. Boundaries and Connections

A special attention was dedicated to the mechanical characterization of the actual supports for the examined curtain wall specimens. At the early design stage, or when no experimental feedback is available, the curtain wall module in Figure 7 should be reasonably described in the form of four point restraints at the corners of the panel. Such a choice would result in reliable calculations for the procedural steps in Figure 6.

A double check and calibration was also carried out for the examined facade modules, based also on the post-process of the available experimental records. On this regard, four axial “discrete” springs were introduced in the Code Aster model, in the region of top and bottom corners, so as to include a certain support flexibility for the restraints of the specimen. The axial stiffness of these springs was calculated with the support of the experimental displacements, given that they proved a certain out-of-plane deformation in the bottom transom. Accordingly, mostly rigid restraints were considered for the top corners (Ktop = 107 kN/m), while for the bottom corners the input stiffness was set in Kbot = 1700 kN/m. Finally, the connection of the glass panel with the supporting frame members was numerically reproduced in the form of a series of equivalent springs with stiffness given by:

where tsil = 10 mm represents the nominal thickness of the silicone joint in use, Esil the modulus [42], while Asil is inclusive of the mesh size/spring influence area.

5.2.5. Damping

In the reference FE model, damping was taken into account with the Rayleigh method, as a function of the mass of the curtain wall module. At first, as also in line with Equation (10), the input value was set in ξ = 8%. The so-calibrated model was thus preliminary taken into account for the 2-DOF characterization in the procedural steps of Figure 6.

Later on, the experimental records were also considered for a post-processing validation of the above assumption (i.e., STEP 7c in Figure 6). Based on the logarithmic decrease of the experimentally measured displacements u(t) for the glass panel:

and

and being T1 the fundamental period of vibration of the curtain wall, the damping was experimentally estimated in a mean value of ξtest = 12% that is in line with the approximate prediction of Equation (10), but also includes local effects that could derive from the impactor itself or possible local damage (i.e., frame, joints). In this context, it is worth mentioning that the effects of the so-derived damping term ξ have minimum effects on the overall dynamic estimates for the curtain wall analysis. On the side of the 2-DOF impact force, in particular, the curtain wall damping proved to have negligible effects on the corresponding time history of the force. On the side of the curtain wall, similarly, the maximum peak of impact effects (i.e., displacements, stresses, etc.) is notoriously not affected by any damping contribution, given that it can be perceived only in the vibrations that follow the instant of the impact. Accordingly, the overall damping estimation from Equation (10) was still found to be reliable.

5.2.6. Impact Load and Impact Area

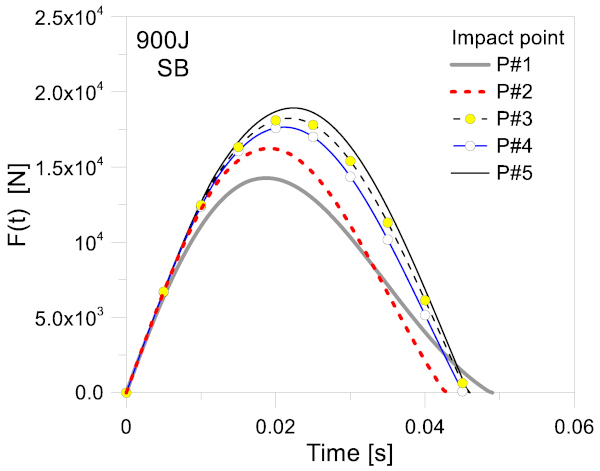
For each experimental configuration in Table 2, the impact load was properly considered in the FE model, based on a number of time histories that were derived from the 2-DOF model in Figure 5 and Figure 6. Given that the input time history modifies with the impact features (impactor, impact point, etc.), the corresponding trends were separately collected for the corresponding FE analyses. Figure 12 shows a typical example of variation of the required input time history, as far as the examined curtain wall is subjected to different impact conditions.

In order to facilitate the calibration of the key parameters for the 2-DOF and the corresponding FE models, the reference impact area was kept constant for all the Code Aster simulations, with a square shape that was set in A = 200 × 200 mm2. The latter, see Figure 13a, was experimentally measured in the case of the TT impactor. Similar experimental acquisitions, see Figure 13b, proved that the TT surface A is mostly half the spheroconical bag. For FE purposes, however, the initial A value was kept fix and the input force was scaled accordingly.

6. Experimental Validation of FE Results

6.1. Impact Response

For the validation of the FE modelling assumptions and the coupled design approach herein proposed (i.e., impactor and contact parameters of the 2-DOF model), the out-of-plane displacements for the three LSn control points were assessed for all the 15 test repetitions. Given that the coupled design approach schematized in Figure 5 and Figure 6 is based on a first vibration mode of the curtain wall object of study, the period was first numerically calculated in T1 = 0.1 s, see Figure 14a.

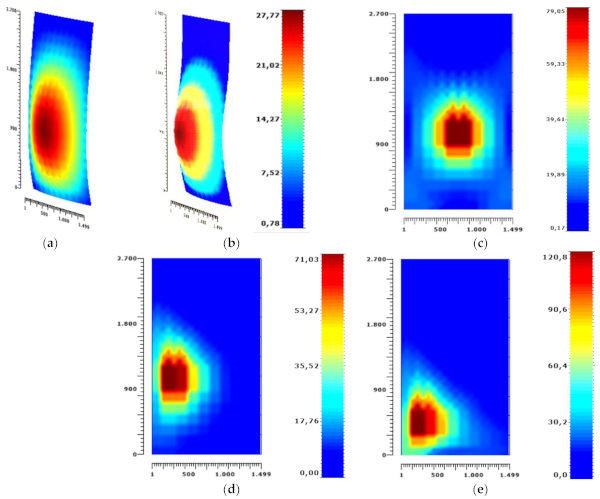
For the curtain wall under various impact conditions, the typical deformed shape was still found to mostly agree with the global vibration mode of the system, see Figure 14b. The corresponding distribution of stress peaks in glass was calculated as in Figure 14c (exposed panel). For the same modular unit under different impact points, additional local effects were observed in major variations about the localization of stress peaks, and some modifications in the global deformation of the visual section (Figure 14d,e).

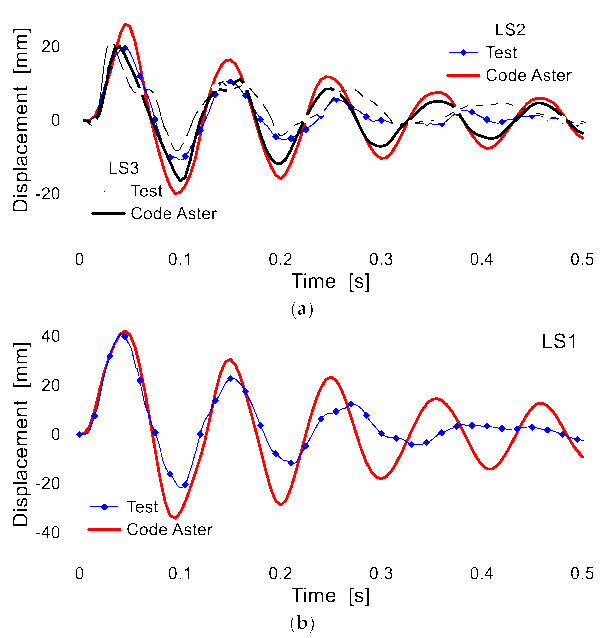
In Figure 15 and Figure 16, selected data are shown for two testing configurations only (SB or TT, with P#1 and Eimp = 900 J). It is of interest that in both the cases, there is a rather good correlation for all the comparative plots, thanks to the reliable input parameters of the coupled approach. For the setup in Figure 15, for example, the maximum response peaks for the visual section under SB impact were quantified in an out-of-plane acceleration of around ≈155 m/s2, with a velocity peak of ≈1.7 m/s, after 0.03–0.05 s of analysis. The corresponding strain peak was measured in ≈0.0008.

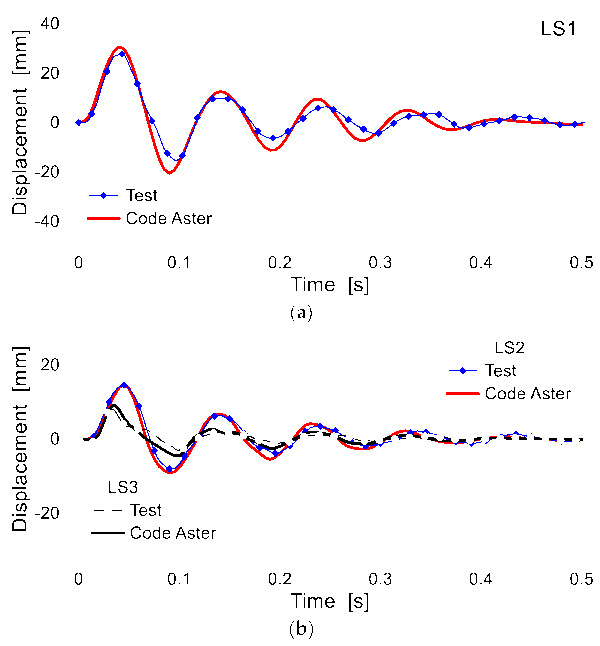
It is worth noting that a general good accuracy was found also for the other testing conditions summarized in Figure 17a, where the numerical peak of out-of-plane displacements at the center of glass (LS1) is proposed under a multitude impact configurations, and compared to the experimental measurements. Given that the drop height, impact point and impactor changes for all the setup configurations, Figure 17a is a further confirmation of the proposal accuracy.

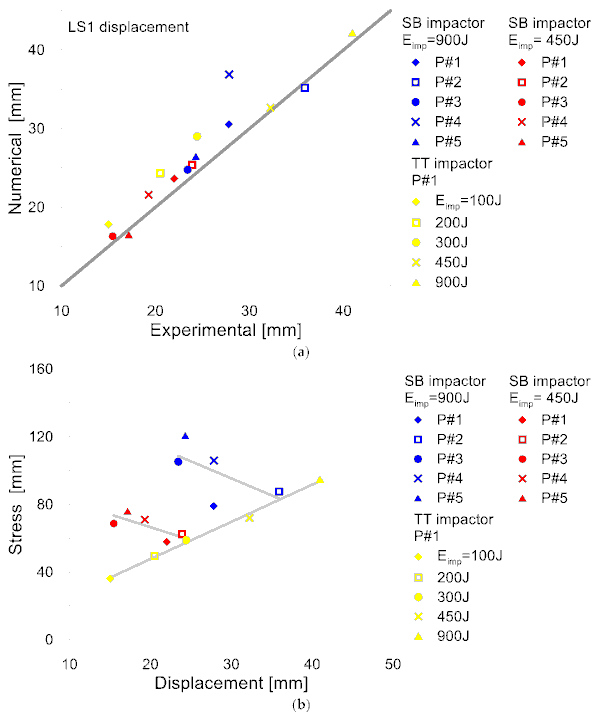
In this regard, it is important to remind that the P#n control points in Figure 17a are implicitly associated to different stiffness parameters and dissipation capacities for the impacted modular unit and for the SB or TT impactor in use.

For few impact configurations only, the FE predictions in Figure 17a tend to overestimate the corresponding experimental measurement. This limitation was justified by the sequence of test repetitions that were carried out on a single modular unit. Especially for few TT scenarios, the laser measurement control point gave evidence of minor damage.

Of interest is also the trend of numerically calculated stress peaks in glass as a function of the deflection amplitude, as schematized in Figure 17b for the panel exposed to impact. For the TT configurations (with P#1 impact point but different impact energy values), as expected, the stress peaks in glass reported in Figure 17b linearly increase with Eimp and the measured deflection peak. When the SB impactor is used, with different Eimp values, a clear correlation still exists between the calculated deflection-stress peaks data, as far as the impact point is kept fix. Moreover, as far as the impact point moves from P#1 towards the edges and the frame of the modular unit, the local stiffness variation results in even higher stress peaks in glass. Regarding the inner glass panel of the IGU visual component, the stress peak for the examined scenarios was numerically estimated in the range from ≈0.3 to ≈0.6 times the values in Figure 17b, depending on the impact configuration.

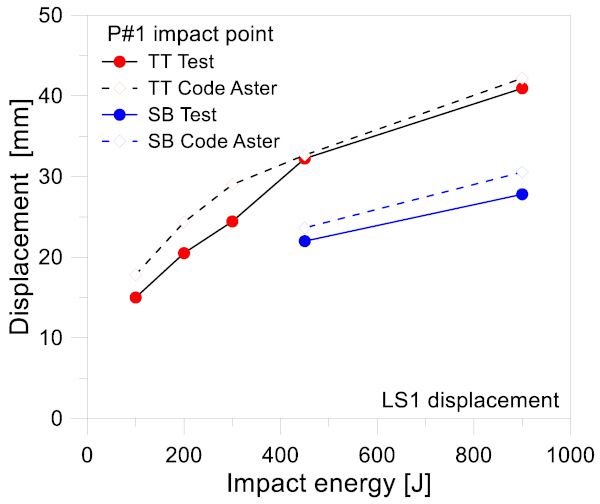
Finally, Figure 18 further confirms the general close correlation of FE estimates with the available experimental data, but also Newman’s assertion in [34] about the higher severity of the TT impactor, for a given impacted body.

6.2. Input Parameters for the Impactor

The key aspect of all the comparisons in Section 6.1 is the use, for the Code Aster numerical model, of input forces that are derived from the 2-DOF model of the system, thus implicitly accounting for the RR coefficient in Equation (6).

In the current study, the parameters for contact (and thus for the impactor features) where calibrated with the support of experimental measurements, as well as the Code Aster estimates. The detailed procedure is shown in Figure 19, as a sub-section of the general approach in Figure 6. The final goal was obtained by matching the deflection peak of each specimen, for all the 15 test repetitions (STEP 7a in Figure 19), and thus minimizing the % scatter Δu for them (STEP 8a), so as to capture a schematic representation of the mechanical behavior for both the TT and the SB impactors (STEP 8b). For the first calibration of impact parameters, major advantage was represented by the available experimental-numerical feedback.

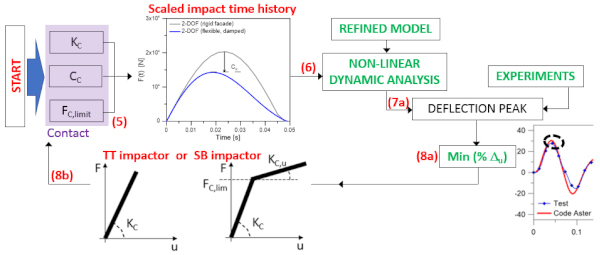
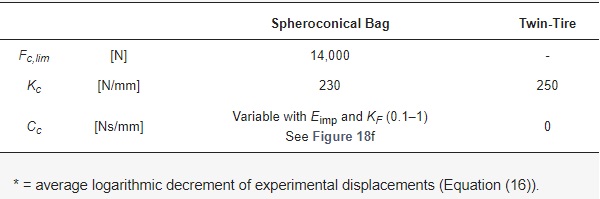
Based on the selected impactors, more in detail, a linear elastic constitutive behavior was taken into account for the tire impactor (thus described in the form of an elastic stiffness KC). No damping was accounted for the TT (CC = 0), as also in line with past literature documents [9,12]. On the other side, to account for the different behavior of the bag, the latter was schematized in the form of an elasto-plastic law with hardening, with input parameters represented by the initial stiffness KC, a limit force FC,limit and a residual stiffness KC,u (with KC,u= 0.9 KC). With the support of benchmark parametric calculations, the limit force FC,limit was introduced in the contact description for the 2-DOF, so as to schematically reproduce the physical impact of the SB pendulum with the curtain wall, and the following separation of the two bodies, due to rebound. Such a plastic force FC,limit was in fact intended to act as a cut-off for the input force that the SB impactor could transfer to the adjacent curtain wall, given that the bag is filled with movable glass spheres.

However, the most influencing parameter for the SB description was represented by the elastic stiffness KC. Accordingly, the iterative calculations were carried out by setting, in the order, KC (with CC = 0), thus FC,limit (with CC = 0, and KC fix) and then CC (with fix KC and FC,limit values). The latter, being susceptible to various parameters on the side of the impacting bodies but also on the impact energy, was calculated in a variable magnitude, as a function of Eimp and KF. In any case, its final value for the SB impactor was usually optimized in the range of ≈0.1–1 Ns/mm, with limited variations for the overall experimental program.

The overall calibration process was based on the minimization of the percentage scatter of the deflection peaks from the FE model and the corresponding experimental records (LS1), under the 15 available testing configurations. The same iterative approach was thus separately repeated for the specimens with TT or SB impactor, so as to obtain a univocal simplified characterization of the two types of impactors. In Table 5, the so-calibrated values are proposed.

Table 5. 2-DOF input parameters for the curtain wall under SBI (with MP = 50 kg and ξtest = 12% *).

In Figure 20, comparative examples are proposed to show the effects of iterative calibrations on the obtained 2-DOF scaled time histories, to further quantify the effects of the various input properties for the SB impactor. As in Figure 20a, the stiffness KC was found responsible of major variations for the corresponding impact forces, while the cut-off force FC,limit generally resulted in less pronounced variations, compared to a perfectly elastic contact (Figure 20b). In terms of damping, the effects of CC are proposed in Figure 20c, while Figure 20d confirms the negligible effect of the curtain wall damping CF. The sensitivity of CC to the impactor velocity or the facade stiffness is finally shown in Figure 20e, where a regular trend can be noticed with vP. On the other side, no clear correlation was found for the stiffness KF (Figure 20f), thus suggesting further explorations.

7. Design Outcomes

7.1. Reduction Coefficient RR

The reduction coefficient in Equations (6) and (7), as earlier discussed, is implicitly accounted for in the scaled time history of impact forces, but depends on various parameters (impactor and impacted body, thus impact rigidity, impact energy, etc.) and it is a key information for design. Given that a combination of the above parameters can separately affect the corresponding reduction coefficient, some parametric calculations are discussed in this paper, in order to emphasize its sensitivity. In Figure 21, the calculated reduction coefficients are compared for the examined curtain wall system under TT (MEPLA and proposed 2-DOF+Code Aster method) or SB (proposed method). As a reference, the impact conditions of Eimp = 100 J, 200 J, 300 J, 450 J or 900 J (P#1) were taken into account. In the case of the SB, values for Eimp = 450 J and 900 J only are reported in Figure 20.

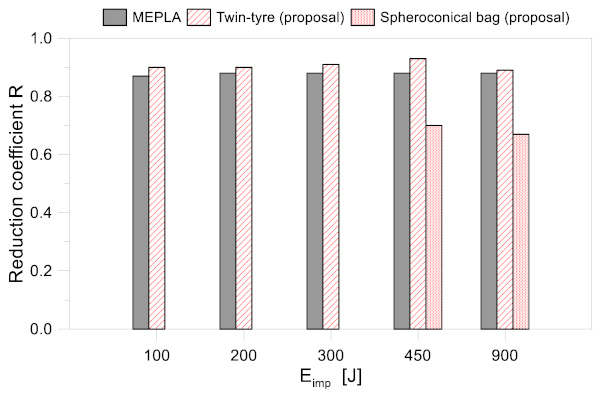
As shown, a first important outcome is that the MEPLA implicit coefficient RMepla is mostly constant under a variable imposed impact energy, and it disregards the impactor features (TT option).

The calculated reduction coefficients RR from the proposed approach, otherwise, clearly modify with the assigned impact conditions, and also diverge from MEPLA estimates. From the 2-DOF+Code Aster calculations, in particular, it is possible to notice that RR tends to decrease as far as Eimp increases for both the TT and SB impactors. This behavior is in line with expectations, given that dissipative phenomena in the impacted curtain wall qualitatively increase under higher input energies. Moreover, the current 2-DOF+Code Aster data in Figure 21 for the TT are close to the unit, compared to the SB. This means that the TT approaches the “ideal” rigid elastic condition of impact. Moreover, this outcome again confirms Newman’s hypothesis about the greater severity of the impact tests carried out with the TT setup (Section 2 and [34]).

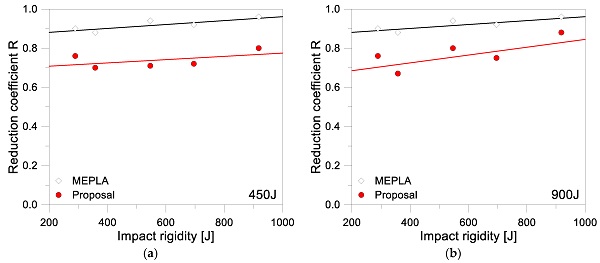
As far as the impact rigidity is also introduced in the parametric comparisons, results agreeing with Figure 22 are obtained. The impact energy is set in Eimp = 450 J or 900 J respectively, while various impact rigidities are taken into account (P#5). Both the MEPLA and 2-DOF+Code Aster trends show a mostly linear variation of the reduction coefficient with the impact rigidity. Besides, the MEPLA twin-tire values overestimate (up to +24%) the corresponding SB coefficients. Again, it is of interest that the MEPLA coefficients in Figure 22 do not change with the imposed Eimp, thus the corresponding calculations can be severely more over-conservative than the reality. Finally, it is possible to notice that the calculated reduction coefficients tend to the unit, as far as the impact stiffness increases. This is because (for relatively stiff impacted bodies) the impact condition is close to an ideal transferred impulse (i.e., on a perfectly rigid surface).

7.2. Iso-Damage Curves

As is known, iso-damage curves are generally very useful for design, given that they provide a fast and reliable feedback for the structural assessment of a given structural system. This is also the case of glass curtain walls under SBI, as far as the iso-damage curves are properly fitted so as to account for various impact parameters.

In this research study, iso-damage curves were developed on the basis of FE simulations carried out with 25 different impact time histories. Major FE results have been extracted and linearly interpolated, for a more accurate description of maximum displacement, maximum tensile principal stress and probability of breakage parameters. A typical example is proposed in Figure 23, where the “proposal” data denote the result of the coupled calculation approach discussed in this paper. In general, the collected results further confirmed that the expected response for a curtain wall panel is not proportionally dependent on the impulse. In addition, as is also in line with the earlier comparisons, it was noticed further the effect of different impactors (TT or SB) on the examined facade module.

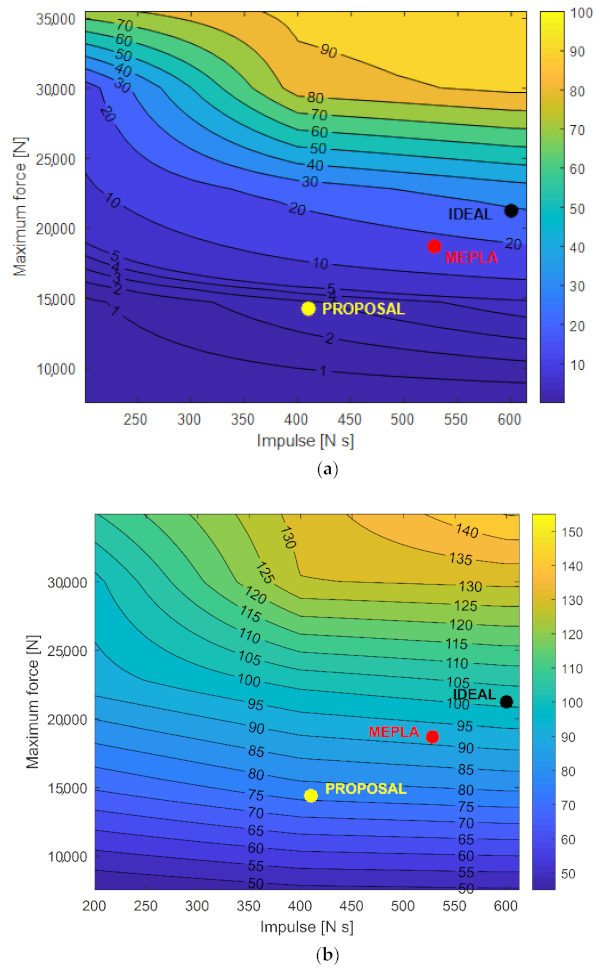
For the facade under SB impactor, it can be noted that the proposed method (already validated by the experimental data) is mostly different from “ideal” and MEPLA assumptions. Given that it proves to properly capture the complex dynamic response of the curtain wall under SBI, it can be used for generalized design problems.

In the case of the curtain wall under TT, the collected comparisons were found to be generally in line with the previous observations. Due to the higher rigidity of the impactor/contact, in the latter case, a close agreement was found also with MEPLA predictions (i.e., due to reduction coefficients tending to the unit, as shown in Figure 19). Besides, the scatter of the so-calculated values from the “ideal” impact conditions were still clearly perceived, thus enforcing the potential of the research approach herein presented, as well as its possible extension to various other configurations of technical interest.

8. Conclusions

The structural design of glass curtain walls is a challenging issue; given that it must satisfy specific performance requirements. Among others, a special care must be paid to the soft body impact (SBI) assessment, where standardized procedures are still required to manufacturers. On one side, the European and German norms introduced the twin-tire (TT) setup and the possibility of numerical simulations in place of experiments. However, several National regulations based on the spheroconical bag (SB) setup are still imposed to producers, and Finite Element (FE) numerical approaches for SB still lack in support of designers. At the same time, the impact response is strongly affected by a multitude of aspects that include the features of the facade (impacted body), the impactor properties and the impact configurations (energy, impact point).

In this paper, the dynamic response of glass curtain walls SBI has been extensively assessed, by taking into account various impact conditions. A special attention has been paid to the SB impactor, towards the calibration of input parameters for the analysis of this demanding setup, to the development of a novel coupled design procedure, by taking advantage of simple full-scale experiments, two Degree of Freedom (2-DOF) calculations and more accurate Finite Element (FE) numerical models for the overall validation of the methodology.

First, the input parameters for the definition of the impact force time history have been proposed. Based on FE numerical model carried out in Code Aster and validated to original experimental results, a refined reduction coefficient RR has been calculated for curtain walls under SB impact. This coefficient, compared to “ideal” impact conditions (rigid facade) further emphasizes the effects of different impact conditions, and thus the possible consequences on the design detailing of curtain walls. In the case of the SB impactor, in particular, it proved to be less severe than the twin-tire, thus enforcing the need of specific studies in support of reliable design procedures. In conclusion, iso-damage curves have been proposed to represent a robust practical tool for design.

Author Contributions

Conceptualization, G.L. and G.M.; software, A.B. and G.L.; validation, A.B., G.L. and C.B.; formal analysis, A.B. and G.L.; investigation, A.B., G.L. and C.B.; writing—original draft preparation, A.B., C.B. and G.M.; writing—review and editing, A.B., G.L., C.B. and G.M.; supervision, G.M. and C.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Additional data will be available upon request.

Acknowledgments

The APCs for the publication of this paper are covered by the “Buildings 2020 Young Investigator Award” granted in January 2021 to the second author. MDPI is gratefully acknowledged. Emanuele Rizzi (University of Trieste) is also gratefully acknowledged for Figure 2b.

Conflicts of Interest

The authors declare no conflict of interest.

References